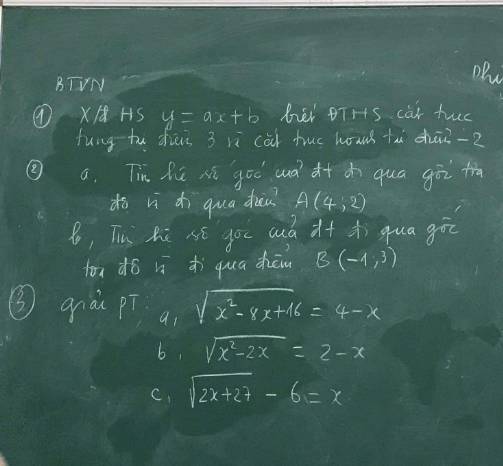Sửa đề:
1) Xác định hàm số y = ax + b \(\left(a\ne0\right)\) biết đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3 và cắt trục hoành tại điểm có hoành độ bằng -2
Giải
Do đồ thị hàm số cắt trục tung đại điểm có tung độ bằng 3 nên b = 3
\(\Rightarrow y=ax+3\)
Do đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -2 nên thay \(x=-2;y=0\) vào hàm số, ta có:
\(a.\left(-2\right)+3=0\)
\(\Leftrightarrow-2a=-3\)
\(\Leftrightarrow a=\dfrac{3}{2}\) (nhận)
Vậy hàm số cần xác định là \(y=\dfrac{3}{2}x+3\)
2)
a) Đồ thị của hàm số đi qua gốc tọa độ có dạng:
\(y=ax\left(a\ne0\right)\)
Do đồ thị hàm số đi qua điểm \(A\left(4;2\right)\) nên thay \(x=4;y=2\) vào hàm số ta có:
\(a.4=2\)
\(a=\dfrac{1}{2}\)
Vậy hệ số góc của đường thẳng cần tìm là \(\dfrac{1}{2}\)
b) Đường thẳng đi qua gốc tọa độ có dạng:
\(y=ax\left(a\ne0\right)\)
Do đường thẳng đi qua điểm \(B\left(-1;3\right)\) nên thay \(x=-1;y=3\) vào đường thẳng, ta có:
\(a.\left(-1\right)=3\)
\(\Leftrightarrow a=-3\)
Vậy hệ số góc cần tìm là \(-3\)
3)
a) ĐKXĐ: \(4-x\ge0\Leftrightarrow x\le4\)
Phương trình tương đương:
\(\sqrt{\left(x-4\right)^2}=4-x\)
\(\Leftrightarrow\left|x-4\right|=4-x\)
\(\Leftrightarrow x-4=4-x\)
\(\Leftrightarrow x+x=4+4\)
\(\Leftrightarrow2x=8\)
\(\Leftrightarrow x=4\) (nhận)
Vậy \(S=\left\{4\right\}\)
b) ĐKXĐ: \(2-x\ge0\Leftrightarrow x\le2\)
Phương trình tương đương:
\(x^2-2x=\left(2-x\right)^2\)
\(\Leftrightarrow\left(x^2-2x\right)-\left(2-x\right)^2=0\)
\(\Leftrightarrow x\left(x-2\right)-\left(x-2\right)^2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right).2=0\)
\(\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\) (nhận)
Vậy \(S=\left\{2\right\}\)
c) \(\sqrt{2x+27}-6=x\)
\(\Leftrightarrow\sqrt{2x+27}=x+6\) (1)
ĐKXĐ: \(x+6\ge0\Leftrightarrow x\ge-6\)
(1) \(\Leftrightarrow2x+27=\left(x+6\right)^2\)
\(\Leftrightarrow2x+27=x^2+12x+36\)
\(\Leftrightarrow x^2+12x+36-2x-27=0\)
\(\Leftrightarrow x^2+10x+9=0\)
\(\Leftrightarrow x^2+x+9x+9=0\)
\(\Leftrightarrow\left(x^2+x\right)+\left(9x+9\right)=0\)
\(\Leftrightarrow x\left(x+1\right)+9\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+9=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\left(tm\right)\\x=-9\left(ktm\right)\end{matrix}\right.\)
Vậy \(S=\left\{-1\right\}\)