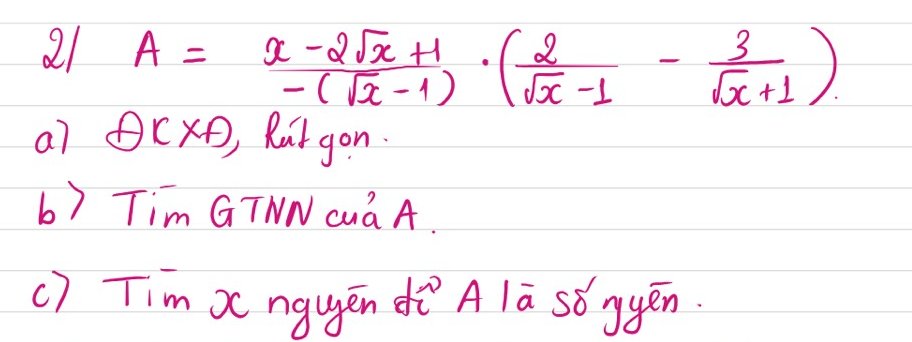\(a)ĐK:\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
\(A=\dfrac{x-2\sqrt{x}+1}{-\left(\sqrt{x}-1\right)}.\left(\dfrac{2}{\sqrt{x}-1}-\dfrac{3}{\sqrt{x}+1}\right)\)
\(=\dfrac{(\sqrt{x}-1)^2}{-\left(\sqrt{x}-1\right)}.\left(\dfrac{2\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=-\left(\sqrt{x}-1\right).\dfrac{2\sqrt{x}+2-3\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=-\dfrac{\left(-\sqrt{x}+5\right)}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(b)A=\dfrac{\sqrt{x}-5}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1-6}{\sqrt{x}+1}=1-\dfrac{6}{\sqrt{x}+1}\)
\(Vì\) \(\sqrt{x}\ge0\Rightarrow\sqrt{x}+1\ge1\Rightarrow\dfrac{6}{\sqrt{x}+1}\le6\Rightarrow A=1-\dfrac{6}{\sqrt{x}+1}\ge1-6=-5\)
Dấu "=" xảy ra \(\Leftrightarrow x=0\)
\(Vậy,A\min\limits=-5\Leftrightarrow x=0_{ }\)
\(c)A=1-\dfrac{6}{\sqrt{x}+1}\in Z\Leftrightarrow\dfrac{6}{\sqrt{x}+1}\in Z\Leftrightarrow\sqrt{x}+1\inƯ\left(6\right)=\left\{1;2;3;6\right\}\)(Vì \(x\ge0;x\in Z\))
\(TH1:\sqrt{x}+1=1\)
\(\Leftrightarrow\sqrt{x}=0\)
\(\Leftrightarrow x=0\left(tm\right)\)
\(TH2:\sqrt{x}+1=2\)
\(\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(loại\right)\)
\(TH3:\sqrt{x}+1=3\)
\(\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\left(tm\right)\)
\(TH4:\sqrt{x}+1=6\)
\(\Leftrightarrow\sqrt{x}=5\Leftrightarrow x=25\left(tm\right)\)
\(Vậy,A\in Z\Leftrightarrow x\in\left\{0;4;25\right\}\)