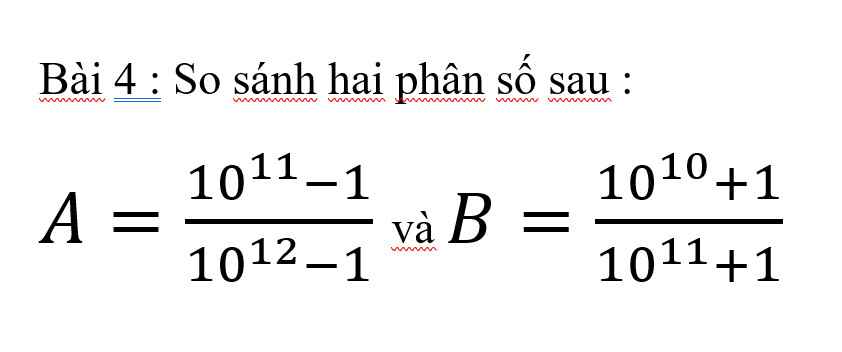\(A=\dfrac{10^{11}-1}{10^{12}-1}\\ 10A=\dfrac{10^{12}-10}{10^{12}-1}\\ 10A=1-\dfrac{9}{10^{12}-1}\\ \)
\(B=\dfrac{10^{10}+1}{10^{11}+1}\\ 10B=\dfrac{10^{11}+10}{10^{11}+1}\\ 10B=1+\dfrac{9}{10^{11}+1}\)
Vì `10^(11)+1<10^(12)-1` nên \(\dfrac{9}{10^{11}+1}>\dfrac{9}{10^{12}-1}\\ \Rightarrow1+\dfrac{9}{10^{11}+1}>1-\dfrac{9}{10^{12}-1}\\ \Rightarrow10B>10A\\ \Rightarrow B>A\)
So sánh 2002/2001 + 2003/2002 + 2001/2003 với 3
Mọi người giúp với ah
tks.
Tìm x biết: 4/x+2=3/2x-1
hãy nêu cách so sánh hai phân số có cùng tử số và hai phân số có cùng mẫu số.
So sánh phân số bằng nhiều cách có thể:
a) 2/5 và 4/7
b) -2/5 và -4/7
a) 2007.2008-1/2007.2008 và 2008.2009-1/2008.2009
làm nhanh và dễ hiểu giúp mik với ^^
So Sánh M và N biết :
M= 10^2020+1/10^2019+1 và N=10^2021+1/10^2020+1
giải nhanh giúp mik với ạ =))
Giúp mk bài 2 với. CẦN RẤT GẤPPPP
So sánh tổng S= \(\dfrac{1}{2}\)+\(\dfrac{2}{2^2}\)+\(\dfrac{3}{2^3}\)+...+\(\dfrac{n}{2^n}\)+...+\(\dfrac{2017}{2^{2017}}\)với 2 (\(n\in N\)*)
so sánh phân số 2023/2022 và 2021/2020
giúp mik vs đúng thì mik sẽ vote cho nhé =))
3,5/2 4/3
