a.
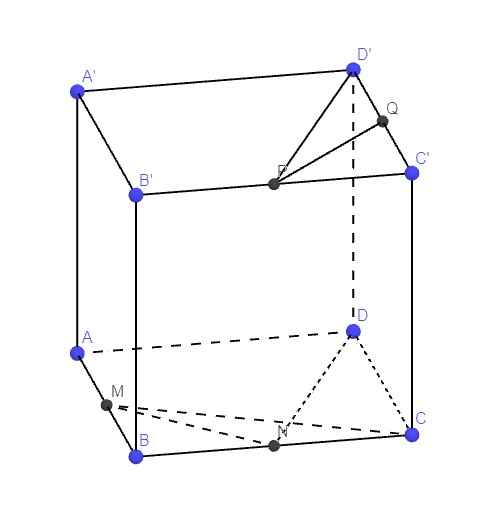
P là trung điểm B'C', Q là trung diểm C'D'
\(\Rightarrow PQ\) là đường trung bình tam giác B'C'D'
\(\Rightarrow PQ||B'D'\Rightarrow PQ||BD\)
\(\Rightarrow\widehat{\left(MN;PQ\right)}=\widehat{\left(MN;BD\right)}\)
Lại có MN là đường trung bình tam giác ABC \(\Rightarrow MN||AC\)
Mà \(AC\perp BD\Rightarrow MN\perp BD\)
\(\Rightarrow\widehat{\left(MN;PQ\right)}=90^0\)
b.
\(D'P||DN\Rightarrow\widehat{\left(CM;D'P\right)}=\widehat{\left(CM;DN\right)}\)
Ta có:
\(\overrightarrow{CM}=\overrightarrow{CB}+\overrightarrow{BM}=\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BA}\)
\(\overrightarrow{DN}=\overrightarrow{DC}+\overrightarrow{CN}=-\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{CB}\)
\(\Rightarrow\overrightarrow{CM}.\overrightarrow{DN}=\left(\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BA}\right)\left(-\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{CB}\right)\)
\(=-\overrightarrow{CB}.\overrightarrow{BA}+\dfrac{1}{2}CB^2-\dfrac{1}{2}BA^2+\dfrac{1}{4}\overrightarrow{BA}.\overrightarrow{CB}\)
\(=\dfrac{1}{2}CB^2-\dfrac{1}{2}BA^2=0\)
\(\Rightarrow CM\perp DN\)
\(\Rightarrow\widehat{\left(CM;D'P\right)}=90^0\)