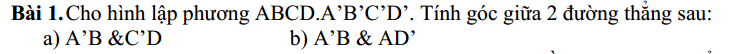a. Do ABCD.A'B'C'D' là hình lập phương
\(\Rightarrow C'D||AB'\)
\(\Rightarrow\) Góc giữa A'B và C'D bằng góc giữa A'B và AB'
Mà \(A'B\perp AB'\) (hai đường chéo hình vuông)
\(\Rightarrow\widehat{\left(A'B;C'D\right)}=90^0\)
b.
Do \(AD'||BC'\) (t/c lập phương)
\(\Rightarrow\widehat{\left(A'B;AD'\right)}=\widehat{\left(A'B;BC'\right)}=\widehat{A'BC'}\)
Mà \(A'B=BC'=A'C'=a\sqrt{2}\) (với a là cạnh lập phương)
\(\Rightarrow\Delta A'BC'\) đều
\(\Rightarrow\widehat{A'BC'}=60^0\)
Đúng 0
Bình luận (0)
