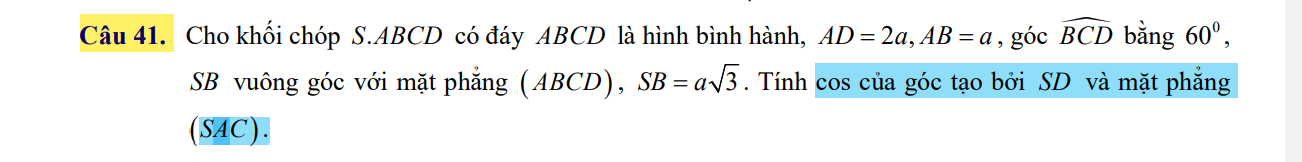Bài 3: Đường thẳng vuông góc với mặt phẳng
Các câu hỏi tương tự
Mọi nguời ơi giúp mình bài này với ạ
Cho hình tứ diện ABCD có ba cạnh AB. BC, BD đôi một vuông góc
1. Chứng minh AB vuông góc mp (ABC)
2. Chứng minh AB vuông góc cạnh CD
3. Chứng minh BC vuông góc mp (ABD)
4.Chứng minh BD vuông góc mp (ABC)
5. chứng minh mp(ABC) vuông góc mp(ABD)
Cho tứ diện SABC có đáy là tam giác đều cạnh a SA vuông góc với đáy SA=2a. Mặt phẳng (P) qua B vuông góc với SC. Diện tích thiết diện tạo bởi (P) với SABC?
mọi người giải giúp ạ !
Cho hình lăng trụ tam giác ABC.ABC. Gọi H là trực tâm của tam giác ABC và biết rằng AH vuông góc với mặt phẳng (ABC). Chứng minh rằng :
a) AAperp BC và AAperp BC
b) Gọi MM là giao tuyến của mặt phẳng (AHA) với mặt bên BCCB, trong đó Min BC,Min BC. Chứng minh rằng tứ giác BCCB là hình chữ nhật và MM là đường cao của hình chữ nhật đó ?
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi H là trực tâm của tam giác ABC và biết rằng A'H vuông góc với mặt phẳng (ABC). Chứng minh rằng :
a) \(AA'\perp BC\) và \(AA'\perp B'C'\)
b) Gọi MM' là giao tuyến của mặt phẳng (AHA') với mặt bên BCC'B', trong đó \(M\in BC,M'\in B'C'\). Chứng minh rằng tứ giác BCC'B' là hình chữ nhật và MM' là đường cao của hình chữ nhật đó ?
Cho tam giác ABC. Gọi left(alpharight) là mặt phẳng vuông góc với đường thẳng CA tại A và left(betaright) là mặt phẳng vuông góc với đường thẳng CB tại B. Chứng minh rằng hai mặt phẳng left(alpharight) và left(betaright) cắt nhau và giao tuyến d của chúng vuông góc với mặt phẳng (ABC) ?
Đọc tiếp
Cho tam giác ABC. Gọi \(\left(\alpha\right)\) là mặt phẳng vuông góc với đường thẳng CA tại A và \(\left(\beta\right)\) là mặt phẳng vuông góc với đường thẳng CB tại B. Chứng minh rằng hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) cắt nhau và giao tuyến d của chúng vuông góc với mặt phẳng (ABC) ?
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a ,tâm O. ΔSABΔSAB đều và nằm trong mặt phẳng vuông góc với (ABCD), I,K lần lượt là trung điểm AB,BC
a) C/m SI⊥(ABCD)SI⊥(ABCD), các ΔSAD,SABΔSAD,SAB đều vuông
b) C/m (SAD)⊥(SAB),(SBC)⊥(SAB),(SDK)⊥(SIC)(SAD)⊥(SAB),(SBC)⊥(SAB),(SDK)⊥(SIC)
C) Tính Cosin của góc (SC,(ABCD)), (BD,(SAB)),(SC,(SAD))
d) tính d(A,(SCD))
#GIÚP MÌNH GIẢI THÍCH RÕ RÀNG VS . MÌNH KO HỌC GIỎI MÔN NÀY, HELP ME PLS
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a ,tâm O. ΔSABΔSAB đều và nằm trong mặt phẳng vuông góc với (ABCD), I,K lần lượt là trung điểm AB,BC
a) C/m SI⊥(ABCD)SI⊥(ABCD), các ΔSAD,SABΔSAD,SAB đều vuông
b) C/m (SAD)⊥(SAB),(SBC)⊥(SAB),(SDK)⊥(SIC)(SAD)⊥(SAB),(SBC)⊥(SAB),(SDK)⊥(SIC)
C) Tính Cosin của góc (SC,(ABCD)), (BD,(SAB)),(SC,(SAD))
d) tính d(A,(SCD))
#GIÚP MÌNH GIẢI THÍCH RÕ RÀNG VS . MÌNH KO HỌC GIỎI MÔN NÀY, HELP ME PLS
Cho hình chóp S.ABCD, có đáy ABCD là hình vuông cạnh a. SA ⊥ (ABCD). SA = a
a. Chứng minh rằng: Các mặt bên của hình chóp đã cho là các tam giác vuông
b. Dựng AM ⊥ SB (M ∈ SB), AN ⊥ SD (N ∈ SD). Chứng minh rằng SC ⊥ (AMN)
c. Gọi K là giao điểm của đường thẳng SC với (AMN). Chứng minh rằng tứ giác AMKN có các đường chéo vuông góc với nhau. Tính diện tích tứ giác đó theo a
cho tứ diện ABCDcó ABC và DBC là hai tam giác đều , gọi I là trung điểm cạch BC.Vẽ đường cao AH của tam giác AID.a) chứng minh BC vuông góc AD và AH vuông góc (BCD) .b)gọi K là trực tâm tam giác AID,chứng minh DK vuông góc AB và AD vuông góc (KBC)
Mọi người giúp mình với
Cho chóp đều Sabcd, SA tạo với mp (abcd), (sbc) các góc bằng nhau, gọi H là hình chiếu của A trên (sbc). Tính SA khi SB=a/2.
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a . Tính góc giữa cạnh bên và mặt đáy .