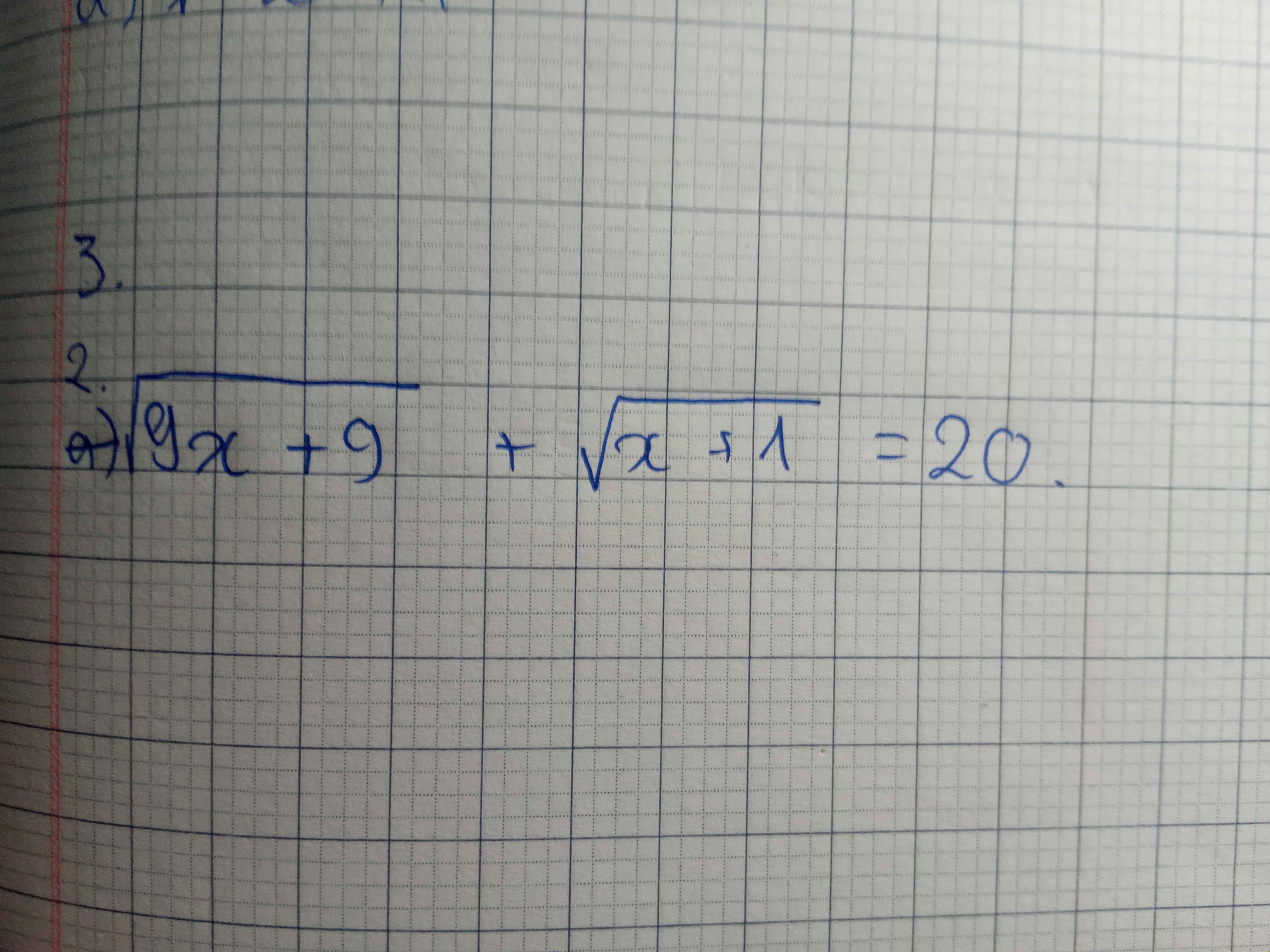Question

Answer 1

\(\sqrt{9\left(x+1\right)}+\sqrt{x+1}\) = 20
\(3\sqrt{x+1}\)+\(\sqrt{x+1}\)=20
\(4\sqrt{x+1}\)=20
\(\sqrt{x+1}\)=5
\(x+1=25\)
\(x=\text{24}\)

Answer 2

Điều kiện xác định:x ≥1 

\(\sqrt{9x+9}+\sqrt{x+1}=20\)

⇔\(9\sqrt{x+1}+\sqrt{x+1}=20\)

⇔\(10\sqrt{x+1}=20\)

⇔\(\sqrt{x+1}=\dfrac{20}{10}\)

⇔\(\sqrt{x+1}=2\)

⇔\(\left(\sqrt{X+1}\right)^2=2^2\)

⇔\(x+1=4\)

⇔\(x=3\left(nhận\right)\)