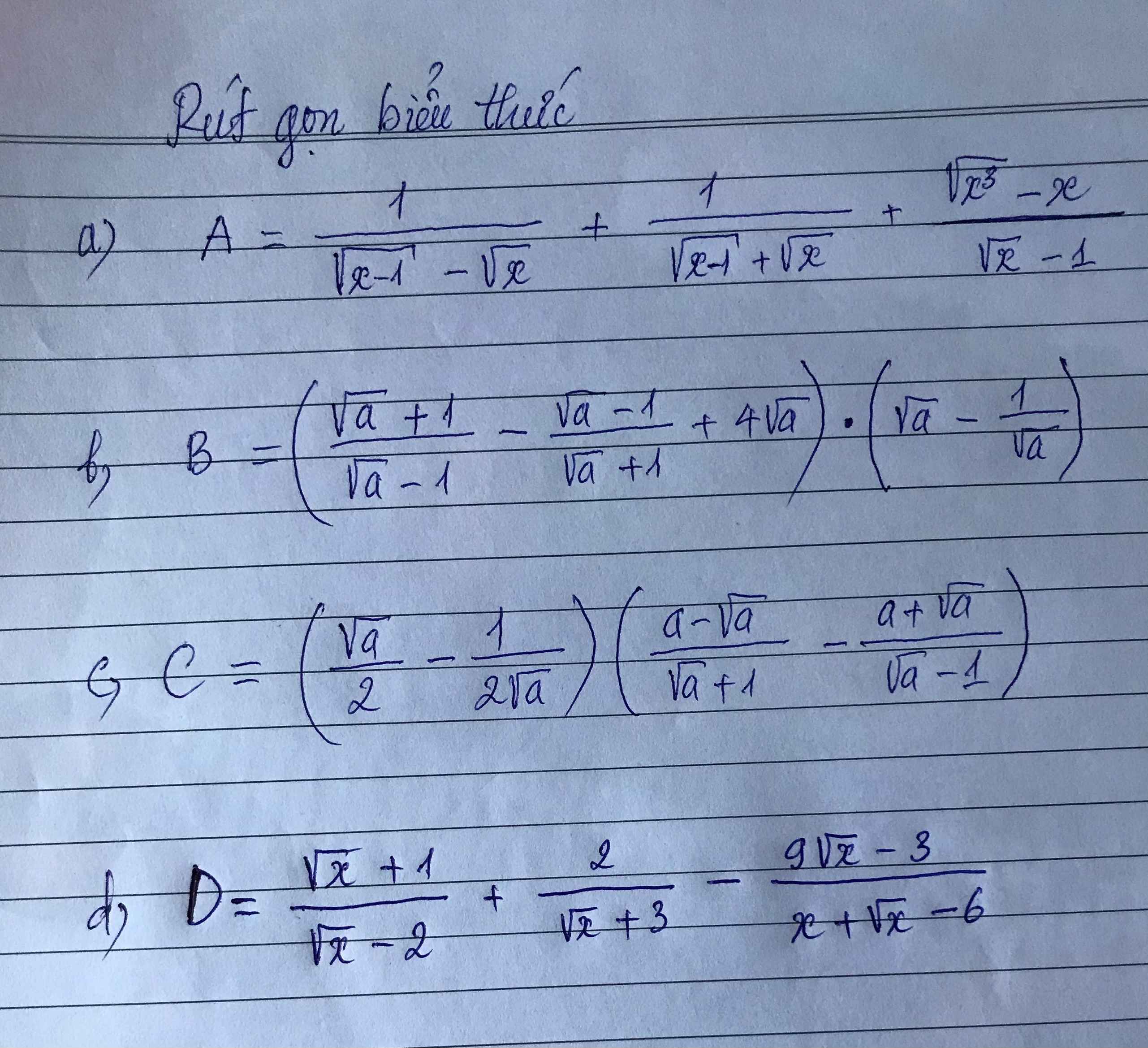a, A=\(\dfrac{1}{\sqrt{x-1}-\sqrt{x}}\)+\(\dfrac{1}{\sqrt{x-1}+\sqrt{x}}\)+\(\dfrac{\sqrt{x^3}-x}{\sqrt{x}-1}\) (ĐKXĐ: x>1)
A=\(\dfrac{1}{\sqrt{x-1}-\sqrt{x}}\)+\(\dfrac{1}{\sqrt{x-1}+\sqrt{x}}\)+\(\dfrac{x\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\)
A=\(-\sqrt{x-1}-\sqrt{x}\)+\(\sqrt{x}-\sqrt{x-1}\)+x
A= x-\(2\sqrt{x-1}\)
b, B=\(\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right)\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\)(ĐKXĐ: a>0, a≠1)
B=\(\left(\dfrac{a+2\sqrt{a}+1}{a-1}-\dfrac{a-2\sqrt{a}+1}{a-1}+4\sqrt{a}\right)\left(\dfrac{a}{\sqrt{a}}-\dfrac{1}{\sqrt{a}}\right)\)
B= \(\left(\dfrac{4\sqrt{a}}{a-1}+\dfrac{4a\sqrt{a}-4\sqrt{a}}{a-1}\right)\dfrac{a-1}{\sqrt{a}}\)
B=\(\dfrac{4a\sqrt{a}}{a-1}\dfrac{a-1}{\sqrt{a}}\)
B=4a
c, C=\(\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)\left(\dfrac{a-\sqrt{a}}{\sqrt{a}+1}-\dfrac{a+\sqrt{a}}{\sqrt{a}-1}\right)\)
(ĐKXĐ: a≥0, a≠1)
C=\(\left(\dfrac{a}{2\sqrt{a}}-\dfrac{1}{2\sqrt{a}}\right)\left(\dfrac{a\sqrt{a}-2a+\sqrt{a}}{a-1}-\dfrac{a\sqrt{a}+2a+\sqrt{a}}{a-1}\right)\)
C=\(\left(\dfrac{a-1}{2\sqrt{a}}\right)\left(\dfrac{-4a}{a-1}\right)\)
C=-2\(\sqrt{a}\)
d, D=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2}{\sqrt{x}+3}-\dfrac{9\sqrt{x}-3}{x+\sqrt{x}-6}\)
(ĐKXĐ: x≥0, x≠4)
D=\(\dfrac{x+4\sqrt{x}+3}{x+\sqrt{x}-6}+\dfrac{2\sqrt{x}-4}{x+\sqrt{x}-6}-\dfrac{9\sqrt{x}-3}{x+\sqrt{x}-6}\)
D=\(\dfrac{x-3\sqrt{x}+2}{x+\sqrt{x}-6}\)
D=\(\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
D=\(\dfrac{\sqrt{x}-1}{\sqrt{x}+3}\)