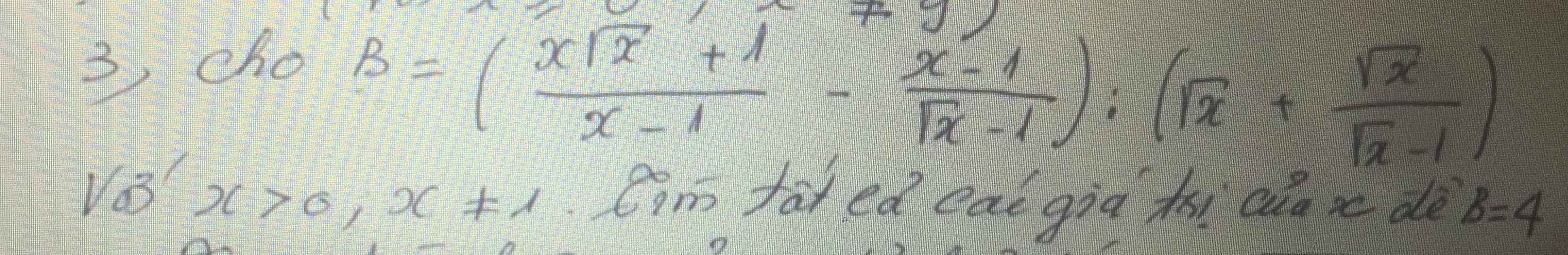ĐK: `x>=0, x \ne 1`.
\(B=\left(\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}-1}\right):\left(\sqrt{x}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\right)\\ =\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}:\dfrac{x-\sqrt{x}+\sqrt{x}}{\sqrt{x}-1}\\ =\dfrac{x-\sqrt{x}+1}{\sqrt{x}-1}.\dfrac{\sqrt{x}-1}{x}\\ =\dfrac{x-\sqrt{x}+1}{x}\)
\(B=4\Leftrightarrow\dfrac{x-\sqrt{x}+1}{x}=4\\ \Leftrightarrow x-\sqrt{x}+1=4x\\ \Leftrightarrow x=\dfrac{7-\sqrt{13}}{18}\)