Question

Answer 1

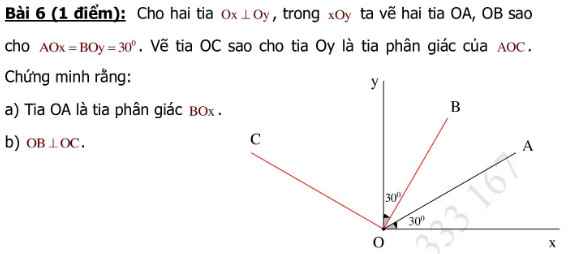
Lời giải:
$\widehat{BOA}=\widehat{xOy}-\widehat{yOB}-\widehat{AOx}$
$=90^0-30^0-30^0=30^0$

Do đó: $\widehat{BOA}=\widehat{AOx}$. Mà $OA$ nằm giữa $Ox$ và $OB$ nên $OA$ là tia phân giác $\widehat{BOx}$

b.

$\widehat{yOB}=\widehat{AOx}=30^0$

$\Rightarrow \widehat{yOB}+\widehat{BOA}=\widehat{AOx}+\widehat{BOA}$

hay $\widehat{yOA}=\widehat{BOx}(1)$

Mà $Oy$ là phân giác $\widehat{COA}$ nên $\widehat{COy}=\widehat{yOA}(2)$

$(1);(2)\Rightarrow \widehat{BOx}=\widehat{COy}$

$\Rightarrow \widehat{BOx}+\widehat{BOy}=\widehat{COy}+\widehat{BOy}$

$\widehat{yOx}=\widehat{COB}$

$90^0=\widehat{COB}$

$\Rightarrow OB\perp OC$