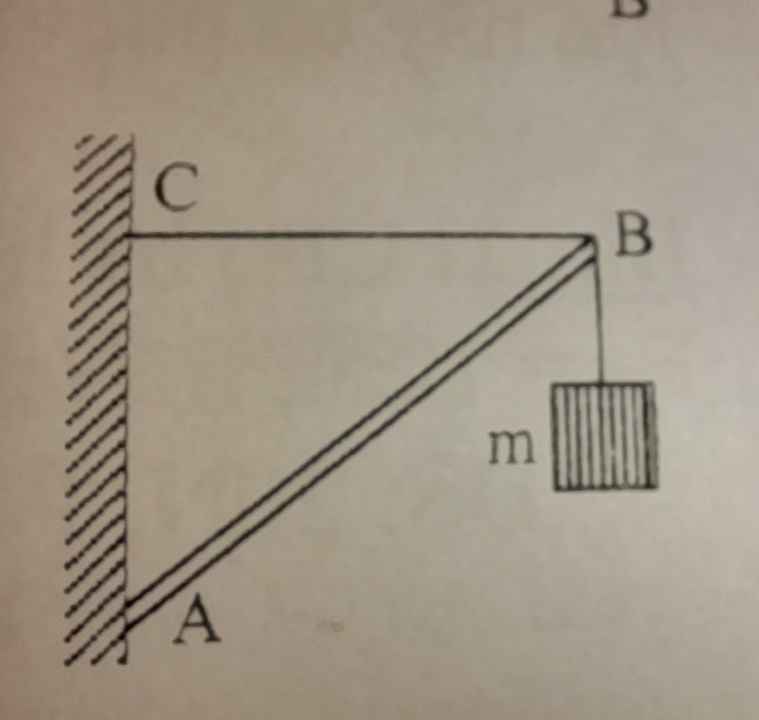
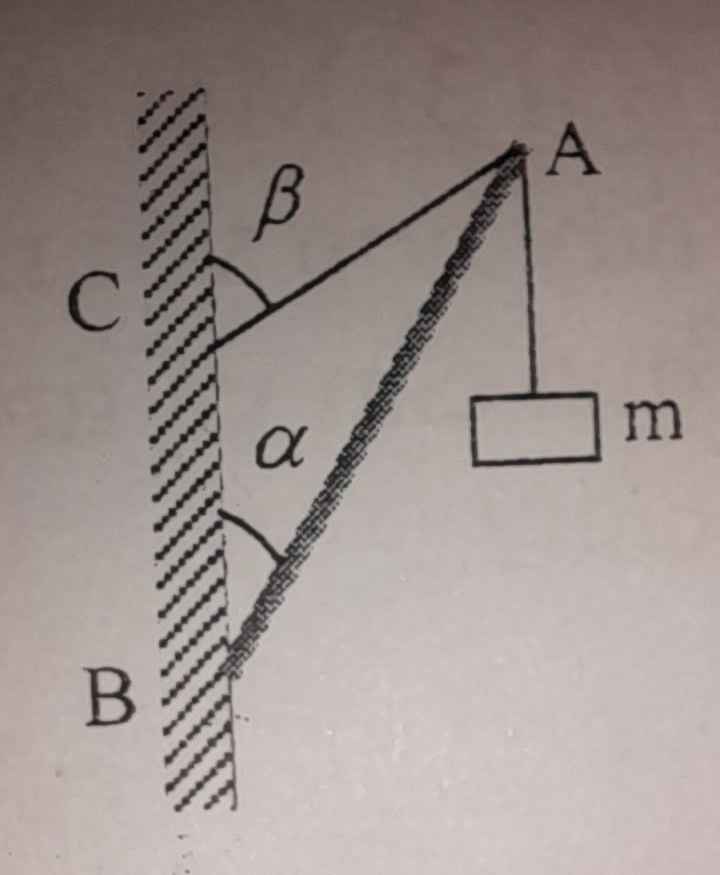
Hai thanh AB, AC được nối nhau và nối cào tường nhờ các bản lề. Tại A có treo vật có trọng lượng P = 1000N. Tìm lực đàn hồi cuất hiện ở các thanh. Cho a+ b = 90°; Bỏ qua trọng lượng các thanh. 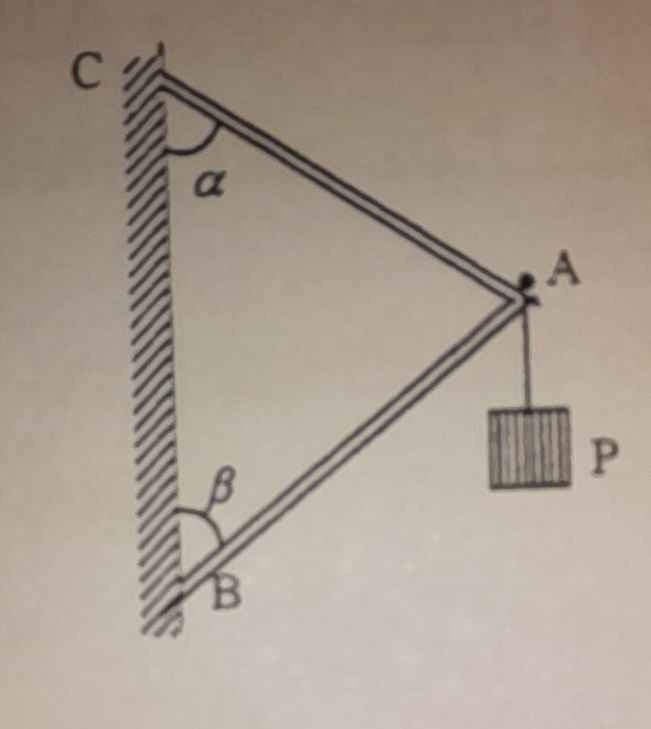
Học tại trường
Chưa có thông tin
Đến từ
Chưa có thông tin , Chưa có thông tin
Số lượng câu hỏi
41
Số lượng câu trả lời
5
Điểm GP
0
Điểm SP
1
Người theo dõi (0)
Đang theo dõi (0)