Tính các số đo x, y trong tam giác dưới đây (H.4.75)
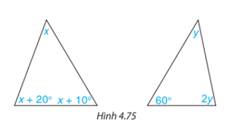
Tính các số đo x, y trong tam giác dưới đây (H.4.75)

Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng\(\widehat {MAN} = \widehat {MBN}\).
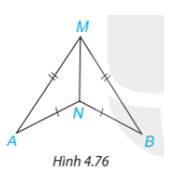
Thảo luận (1)Hướng dẫn giảiXét \(\Delta MNA\) và \(\Delta MNB \) có:
AM=BM (gt)
AN=BN (gt)
MN chung
=>\(\Delta MNA = \Delta MNB\) (c.c.c)
=>\(\widehat {MAN} = \widehat {MBN}\) (2 góc tương ứng)
(Trả lời bởi Hà Quang Minh)
Trong Hình 4.77, có AO = BO,\(\widehat {OAM} = \widehat {OBN}\). Chứng minh rằng AM = BN.
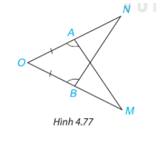
Thảo luận (1)Hướng dẫn giảiXét 2 tam giác OAM và OBN có:
\(\widehat {OAM} = \widehat {OBN}\) (gt)
AO=BO (gt)
\(\widehat{O}\) chung
=>\(\Delta OAM = \Delta OBN\)(g.c.g)
=>AM=BN (2 cạnh tương ứng)
(Trả lời bởi Hà Quang Minh)
Trong Hình 4.78, ta có AN = BM,\(\widehat {BAN} = \widehat {ABM}\). Chứng minh rằng\(\widehat {BAM} = \widehat {ABN}\).
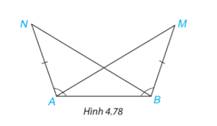
Thảo luận (1)Hướng dẫn giảiXét \(\Delta ANB \) và \(\Delta BMA\) có:
AN=BM (gt)
\(\widehat {BAN} = \widehat {ABM}\) (gt)
AB chung
=>\(\Delta ANB = \Delta BMA\)(c.g.c)
=> \(\widehat{ABN} = \widehat{BAM}\) (2 góc tương ứng)
(Trả lời bởi Hà Quang Minh)
Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Chứng minh rằng MB = NB và góc AMB bằng góc ANB.
Thảo luận (1)Hướng dẫn giải
Vì M, N nằm trên đường trung trực của AB nên MA = MB ; NA = NB ( tính chất)
Mà MA = NA (gt)
Do đó, MA = NA = MB = NB.
Xét tam giác AMB và tam giác ANB có:
MA = NA (gt)
MB = NB (cmt)
AB chung
Do đó, ∆AMB = ∆ANB (c – c – c).
\(\Rightarrow \widehat{AMB}=\widehat{ANB}\) (2 góc tương ứng).
Vậy MB = NB và góc AMB bằng góc ANB.
(Trả lời bởi Kiều Sơn Tùng)
Cho tam giác ABC cân tại A có \(\widehat {A{\rm{ }}} = 120^\circ \). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
a) \(\Delta \)BAM = \(\Delta \)CAN;
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
Thảo luận (1)Hướng dẫn giải
a) Xét 2 tam giác vuông BAM và CAN có:
\(\widehat{BAM} = \widehat{CAM}(=90^0)\)
AB=AC (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
=>\(\Delta BAM = \Delta CAN\)(g.c.g)
b) Cách 1:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat {B} + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\)
Xét tam giác MAC có:
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
\(\Rightarrow \) Tam giác AMC cân tại M.
Vì \(\Delta BAM = \Delta CAN\)
=> BM=CN ( 2 cạnh tương ứng)
=> BM+MN=CN+NM
=> BN=CM
Xét 2 tam giác ANB và AMC có:
AB=AC (cmt)
\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))
BN=MC (cmt)
=>\(\Delta ANB = \Delta AMC\)(c.c.c)
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
Cách 2:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\)
Vì \(\Delta BAM = \Delta CAN\) nên AM = AN (2 cạnh tương ứng)
=> \(\Delta AMN\) đều (Tam giác cân có 1 góc bằng 60 độ)
=> \(\widehat {NAM}=60^0\)
Ta có: \(\widehat{BAN}+\widehat{NAM}=\widehat{BAM}\)
=> \(\widehat{BAN} + 60^0=90^0\)
=> \(\widehat{BAN}=30^0\)
Xét tam giác ABN có \(\widehat{BAN}=\widehat{ABN}(=30^0\) nên \(\Delta ABN\) cân tại N.
Ta có: \(\widehat{CAM}+\widehat{NAM}=\widehat{CAN}\)
=> \(\widehat{CAM} + 60^0=90^0\)
=> \(\widehat{CAM}=30^0\)
Xét tam giác ACM có \(\widehat{CAM}=\widehat{ACM}(=30^0\) nên \(\Delta ACM\) cân tại M.
(Trả lời bởi Kiều Sơn Tùng)
Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho \(\widehat {CAM} = {30^o}\). Chứng minh rằng:
a) Tam giác CAM cân tại M;
b) Tam giác BAM là tam giác đều;
c) M là trung điểm của đoạn thẳng BC.
Thảo luận (1)Hướng dẫn giải
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Do đó, MB = MC. Mà M nằm giữa B và C
=> M là trung điểm của BC.
(Trả lời bởi Kiều Sơn Tùng)