a) Sử dụng máy tính cầm tay bấm liên tiếp các nút
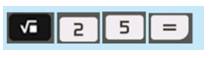
Em hãy đọc kết quả x trên màn hình rồi tính x2.
b) Sử dụng máy tính cầm tay bấm liên tiếp các nút

Em hãy đọc kết quả x trên màn hình rồi tính x2.

a) Sử dụng máy tính cầm tay bấm liên tiếp các nút

Em hãy đọc kết quả x trên màn hình rồi tính x2.
b) Sử dụng máy tính cầm tay bấm liên tiếp các nút

Em hãy đọc kết quả x trên màn hình rồi tính x2.

Dùng máy tính cầm tay để tính các căn bậc hai số học sau:
\(\sqrt 3 ;\,\sqrt {15\,\,129} ;\,\sqrt {10\,\,000} ;\,\sqrt {10} \).
Thảo luận (1)Hướng dẫn giải\(\sqrt 3 \approx 1,732...;\,\sqrt {15\,\,129} \, = 123;\,\,\,\,\,\,\sqrt {10\,\,000} = 100;\,\,\,\sqrt {10} \approx 3,162...\)
(Trả lời bởi Hà Quang Minh)
Hoàn thành các phát biểu sau:
a) Số a=5,123 là một số thập phân hữu hạn nên a là số .?.
b) Số b = 6,15555... = 6,1(5) là một số thập phân vô hạn tuần hoàn nên b là số .?.
c) Người ta chứng minh được \(\pi= 3,14159265...\) là một số thập phân vô hạn không tuần hoàn. Vậy \(\pi\) là số ?.
d) Cho biết số c=2,23606... là một số thập phân vô hạn không tuần hoàn. Vậy c là số .?.
Thảo luận (1)Hướng dẫn giảia) Số a=5,123 là một số thập phân hữu hạn nên a là số hữu tỉ
b) Số b = 6,15555... = 6,1(5) là một số thập phân vô hạn tuần hoàn nên b là số hữu tỉ
c) Người ta chứng minh được \(\pi= 3,14159265...\) là một số thập phân vô hạn không tuần hoàn. Vậy \(\pi\) là số vô tỉ
d) Cho biết số c=2,23606... là một số thập phân vô hạn không tuần hoàn. Vậy c là số vô tỉ
(Trả lời bởi Hà Quang Minh)
Tính độ dài cạnh của một mảnh đất hình vuông có diện tích là 169 m2
Thảo luận (1)Hướng dẫn giảiĐộ dài cạnh là: \(\sqrt {169} = 13\)(m)
(Trả lời bởi Hà Quang Minh)
a) Tìm giá trị của x2 với x lần lượt bằng 2; 3; 4; 5; 10.
b) Tìm số thực không âm x với x2 lần lượt bằng 4; 9; 16; 25; 100.
Thảo luận (1)Hướng dẫn giảia) x = 2, ta được x2 = 4;
x =3, ta được x2 = 9;
x = 4, ta được x2 = 16;
x =5, ta được x2 = 25;
x = 10, ta được x2 = 100.
b) x2 = 4, ta được x = 2;
x2 = 9, ta được x = 3;
x2 = 16, ta được x = 4;
x2 = 25, ta được x = 5;
x2 = 100, ta được x = 10.
(Trả lời bởi Hà Quang Minh)
Cho hai hình vuông ABCD và AMBN như hình bên. Cho biết cạnh AM=1 dm.
- Em hãy cho biết diện tích hình vuông ABCD gấp mấy lần diện tích hình vuông AMBN.
- Tính diện tích hình vuông ABCD.
- Hãy biểu diễn diện tích hình vuông ABCD theo độ dài đoạn AB.
Thảo luận (1)Hướng dẫn giải- Các tam giác AMB, ABN, AND, DNC, CNB có diện tích bằng nhau.
Diện tích hình vuông AMCD bằng 2 lần diện tích tam giác ANB, diện tích hình vuông ABCD bằng 4 lần diện tích tam giác ANB nên
Diện tích hình vuông ABCD gấp 2 lần diện tích hình vuông AMCD.
- Diện tích hình vuông ABCD là: 2.12=2 (dm2)
- Diện tích hình vuông ABCD bằng AB2
(Trả lời bởi Hà Quang Minh)
Hãy biểu diễn các số hữu tỉ sau đây dưới dạng số thập phân: \(\frac{{12}}{{25}};\frac{{27}}{2};\frac{{10}}{9}\)
Thảo luận (1)Hướng dẫn giải\(\frac{{12}}{{25}} = 0,48;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{27}}{2} = 13,5;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{10}}{9} = 1,(1)\)
(Trả lời bởi Hà Quang Minh)
Hãy thực hiện các phép chia sau đây:
\(3:2 = ?\,\,\,\,\,\,\,\,\,\,\,37:25 = ?\,\,\,\,\,\,\,\,5:3 = ?\,\,\,\,\,\,1:9 = ?\)
b) Dùng kết quả trên để viết các số \(\frac{3}{2};\frac{{37}}{{25}};\frac{5}{3};\frac{1}{9}\) dưới dạng số thập phân.
Thảo luận (1)Hướng dẫn giảia)\(3:2 = 1,5\,\,\,\,\,\,\,\,\,\,\,37:25 = 1,48\,\,\,\,\,\,\,\,5:3 = 1,666...\,\,\,\,\,\,1:9 = 0,111...\)
b) \(\frac{3}{2} = 1,5;\,\,\,\,\frac{{37}}{{25}} = 1,48;\,\,\,\,\frac{5}{3} = 1,666...;\,\,\,\frac{1}{9} = 0,111...\)
Chú ý: Các phép chia không bao giờ dừng ta viết ba chữ số thập phân sau dấu phẩy và sau đó thêm dấu ba chấm phía sau.
(Trả lời bởi Hà Quang Minh)
Hãy so sánh hai số hữu tỉ: \(0,834\) và \(\frac{5}{6}\).
Thảo luận (1)Hướng dẫn giảiTa có \(\frac{5}{6} = 0,8(3)\) = \(0,8333....\)
Vì:\(0,834 > 0,8333... \Rightarrow 0,834 > \frac{5}{6}\)
(Trả lời bởi Hà Quang Minh)
Viết các căn bậc hai số học của: 16; 7; 10; 36.
Thảo luận (1)Hướng dẫn giảiCăn bậc hai số học của: 16; 7; 10; 36 lần lượt là: \(4;\,\sqrt 7 ;\,\sqrt {10} ;\,6\)
(Trả lời bởi Hà Quang Minh)