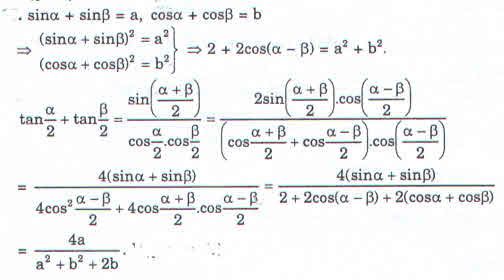
Nếu \(\sin\alpha+\sin\beta=a;\cos\alpha+\cos\beta=b;\left(\left|a\right|\le\sqrt{2};\left|b\right|\le\sqrt{2}\right)\) thì biểu thức \(\tan\dfrac{\alpha}{2}+\tan\dfrac{\beta}{2}\) có giá trị tính theo a và b là
\(\dfrac{2a}{a^2+b^2+b}\).\(\dfrac{2b}{a^2+b^2+a}\).\(\dfrac{4a}{a^2+b^2+2b}\).\(\dfrac{4a}{a^2+b^2+2a}\).Hướng dẫn giải: