Cho tam giác ABC nội tiếp đường tròn (O). Biết BC = 2cm, \(\widehat{A}=45^o\).
Khẳng định nào sau đây là sai?
Diện tích hình tròn (O) bằng \(2\pi\left(cm^2\right)\). Diện tích của hình viên phân viên giới hạn của dây BC và cung nhỏ BC là \(S_{vp}=\dfrac{\pi-2}{2}\left(cm^2\right)\). Diện tích tam giác OBC là \(1cm^2\). AC = BC. Hướng dẫn giải: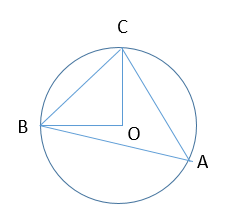
Có \(\widehat{BAC}=45^o\Rightarrow\widehat{BOC}=90^o\).
Ta có: \(OB^2+OC^2=BC^2\)\(\Leftrightarrow2r^2=2^2\)\(\Leftrightarrow r=\sqrt{2}\) (r là bán kính đường tròn (O)).
Diện tích đường tròn (O) là: \(r^2\pi=\left(\sqrt{2}\right)^2\pi=2\pi\left(cm^2\right)\).
Diện tích cung BC là:
\(\dfrac{1}{4}.2\pi=\dfrac{\pi}{2}\left(cm^2\right)\)
Diện tích tam giác OBC là: \(\dfrac{1}{2}OB.OC=\dfrac{1}{2}.\sqrt{2}.\sqrt{2}=1\left(cm^2\right)\).
Diện tích hình viên phân giới hạn của dây BC và cung nhỏ BC là: \(\dfrac{\pi}{2}-1\left(cm^2\right)\).

