Cho tam giác ABC có \(\widehat{A}=70^0\). Các đường phân giác BE, CD của tam giác cắt nhau tại I. Tính số đo \(\widehat{BIC}\)?
\(125^0\).\(100^0\).\(105^0\).\(140^0\).Hướng dẫn giải: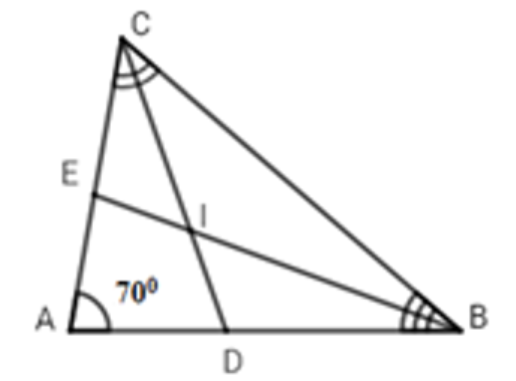
Do BE, CD là phân giác của góc B và góc C
nên \(\widehat{IBC}=\dfrac{\widehat{ABC}}{2};\widehat{ICB}=\dfrac{\widehat{ACB}}{2}\)
\(\Rightarrow\widehat{IBC}+\widehat{ICB}=\dfrac{\widehat{ABC}+\widehat{ACB}}{2}=\dfrac{180^0-\widehat{A}}{2}\)
\(\Rightarrow\widehat{IBC}+\widehat{ICB}=\dfrac{180^0-70^0}{2}=55^0\)
Xét trong tam giác IBC có \(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^0\)
\(\Rightarrow\widehat{BIC}=180^0-55^0=125^0\)

