Bài 7: Tứ giác nội tiếp

Cho nửa đường tròn đường kính AB. Lấy hai điểm C và D trên nửa đường tròn sao cho \(\stackrel\frown{AC}=\stackrel\frown{CD}=\stackrel\frown{DB}\).
Các tiếp tuyến từ B và C của nửa đường cắt nhau tại I. Hai tia AC và BD cắt nhau tại K. Khẳng định nào dưới đây là sai?

Tam giác KAB và tam giác IBC đều. \(\widehat{KBI}=30^o\). Tứ giác KIBC nội tiếp.  Tam giác KIB vuông. \(\widehat{KCI}=60^o\). Hướng dẫn giải:

​
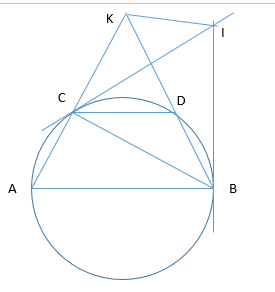
Các tam giác KAB và tam giác CIB cân và có một góc bằng \(60^o\) nên đều là tam giác đều.
Suy ra: \(\widehat{CKB}=\widehat{CIB}=60^o\) mà hai góc này cùng chắn cung BC nên tứ giác KICB nội tiếp.
Có \(\widehat{BCA}=90^o\Rightarrow\widehat{KCB}=90^o\) nên \(\widehat{KIB}=90^o\).
Vậy tam giác KIB vuông tại I.
\(\widehat{KBI}=\frac{1}{2}sđ\stackrel\frown{BD}=30^o\).
\(\widehat{KCI}=\widehat{IBK}=30^o\).