Bài tập cuối chương IV
Nội dung lý thuyết
1. Đặc điểm
| Hình | Đặc điểm |
| Tam giác đều | - Có ba cạnh bằng nhau. - Có ba góc bằng nhau và bằng 60o. |
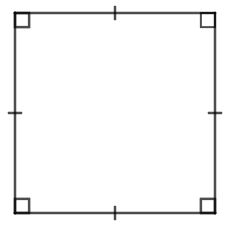
| Hình vuông | - Bốn cạnh bằng nhau. - Bốn góc bằng nhau và bằng 90o. - Hai đường chéo bằng nhau. |
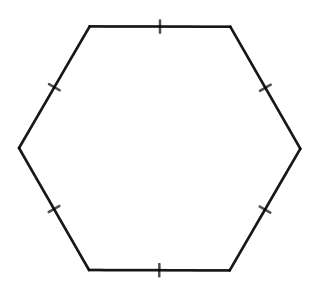
| Lục giác đều | - Sáu cạnh bằng nhau. - Sáu góc bằng nhau và bằng 120o. - Ba đường chéo chính bằng nhau. - Sáu đường chéo phụ bằng nhau. |
| Hình chữ nhật | - Bốn góc bằng nhau và bằng 90o. - Các cạnh đối bằng nhau. - Hai đường chéo bằng nhau. |
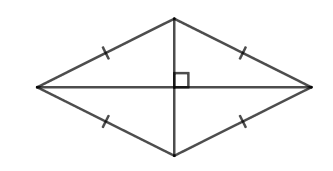
| Hình thoi | - Bốn cạnh bằng nhau. - Hai đường chéo vuông góc với nhau. - Các cạnh đối song song với nhau. - Các góc đối bằng nhau. |
| Hình bình hành | - Các cạnh đối bằng nhau. - Hai đường chéo cắt nhau tại trung điểm mỗi đường. - Các cạnh đối song song với nhau. - Các góc đối bằng nhau. |
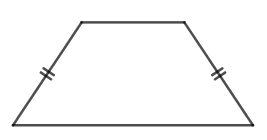
| Hình thang cân | - Hai cạnh bên bằng nhau. - Hai đường chéo bằng nhau. - Hai cạnh đáy song song với nhau. - Hai góc kề một đáy bằng nhau. |
2. Chu vi và diện tích của các hình
| Tên hình | Hình vẽ | Chu vi | Diện tích |
| Tam giác đều |
| \(C=3a\) (a là cạnh của tam giác) | \(S=\dfrac{1}{2}a.h\) (h là chiều cao) |
| Hình vuông |
| \(C=4a\) (a là cạnh của hình vuông) | \(S=a.a\) |
| Lục giác đều |
| \(C=6a\) (a là cạnh của lục giác) | |
| Hình chữ nhật |
| \(C=2\left(a+b\right)\) (a, b là độ dài hai cạnh) | \(S=a.b\) |
| Hình thoi |
| \(C=4a\) (a là độ dài cạnh của hình thoi) | \(S=\dfrac{1}{2}.m.n\) (m, n là độ dài hai đường chéo của hình thoi) |
| Hình bình hành |
| \(C=2\left(a+b\right)\) (a, b là độ dài hai cạnh) | \(S=a.h\) (h là chiều cao ứng với cạnh a) |
| Hình thang cân |
| \(C=a+b+2c\) (a, b, c lần lượt là độ dài đáy bé, đáy lớn, cạnh bên của hình thang cân) | \(S=\dfrac{1}{2}.\left(a+b\right).h\) (h là chiều cao của hình thang) |

.png)