Bài 8: Đối xứng tâm
Nội dung lý thuyết
1. Hai điểm đối xứng qua một điểm
Cho điểm \(A\) và điểm \(O\) tùy ý. Vẽ điểm \(A'\) sao cho \(O\) là trung điểm \(AA'\).

Khi đó, ta gọi \(A'\) là điểm đối xứng với \(A\) qua điểm \(O\), \(A\) là điểm đối xứng của \(A'\) qua \(O\), hai điểm \(A\) và \(A'\) là hai điểm đối xứng nhau qua \(O\).
Định nghĩa: Hai điểm được gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm đoạn thẳng nối hai điểm đó.
Quy ước: Điểm đối xứng với điểm \(O\) qua \(O\) cũng là điểm \(O\).
2. Hai hình đối xứng qua một điểm
Xét ví dụ: Cho đoạn thẳng \(AB\) và một điểm \(O\). Vẽ \(A',B'\) lần lượt là điểm đối xứng của \(A,B\) qua \(O\).
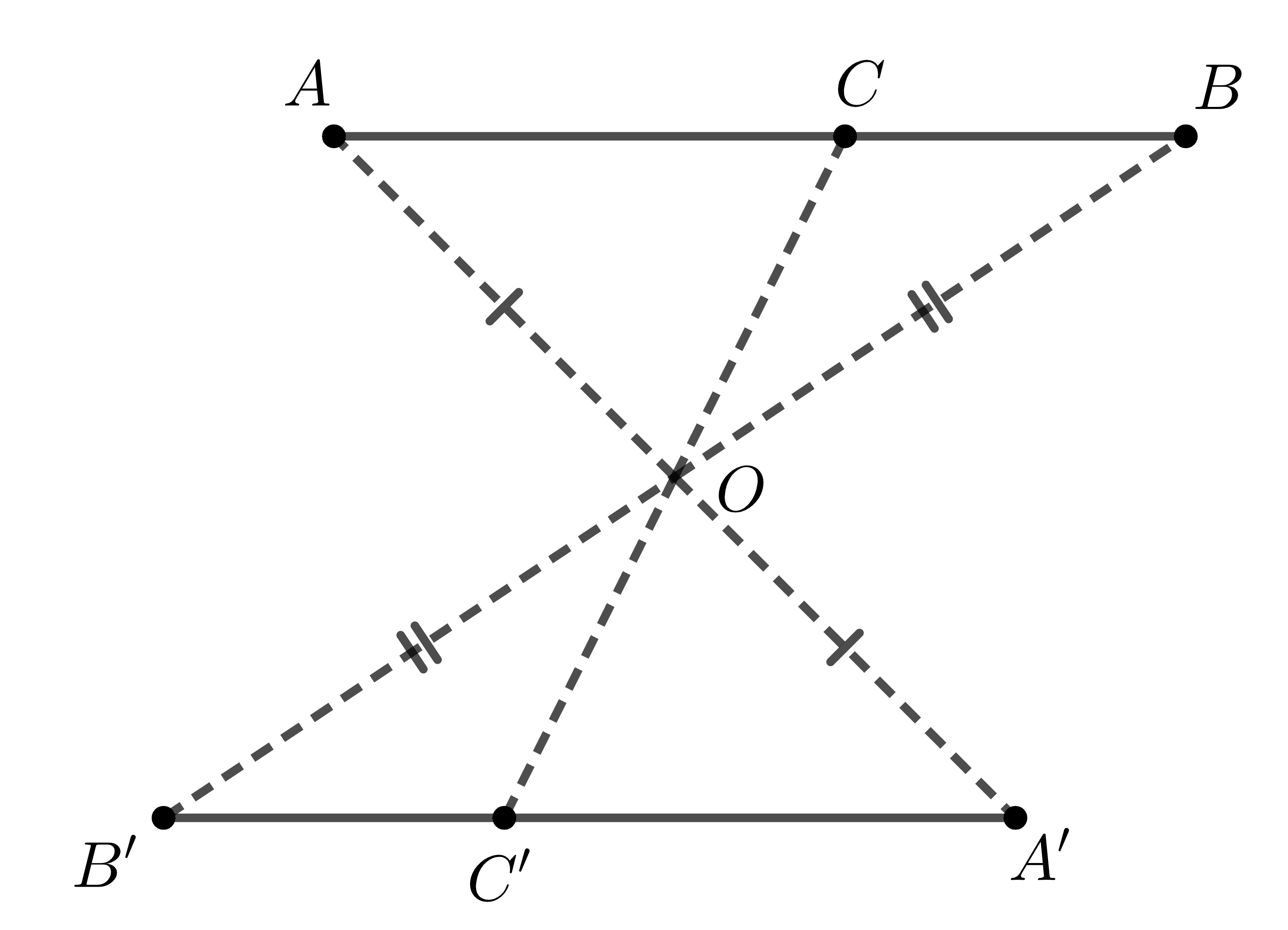
Lấy điểm \(C\in AB\). Vẽ điểm \(C'\) đối xứng với \(C\) qua \(O\), ta thấy \(C'\in A'B'\).
Ta nói: Hai đoạn thẳng \(AB\) và \(A'B'\) là hai đoạn thẳng đối xứng nhau qua điểm \(O\).
Định nghĩa: Hai hình được gọi là đối xứng với nhau qua điểm \(O\) nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua điểm \(O\) và ngược lại.
Khi đó, điểm \(O\) được gọi là tâm đối xứng của hai hình đó.
Người ta chứng minh được kết quả sau:
Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.
Ví dụ:
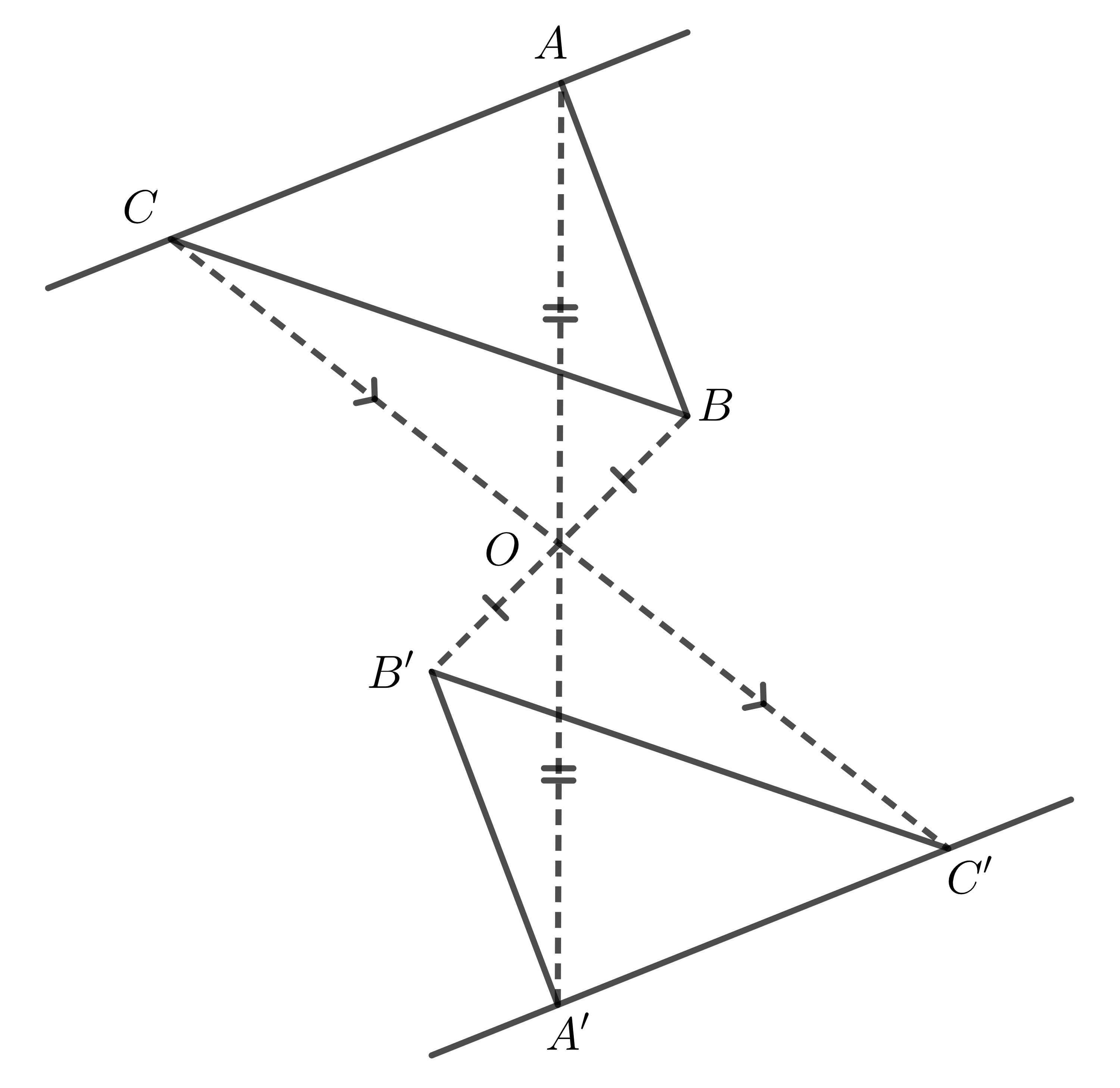
Trong hình trên, ta có:
- Hai đoạn thẳng \(AB,A'B'\) đối xứng với nhau qua \(O\).
- Hai đường thẳng \(AC,A'C'\) đối xứng với nhau qua \(O\).
- Hai góc \(ABC,A'B'C'\) đối xứng với nhau qua \(O\).
- Hai tam giác \(ABC,A'B'C'\) đối xứng với nhau qua \(O\).
Do đó ta có: \(\left\{ \begin{array} $AB=A'B'\\\widehat{ABC}=\widehat{A'B'C'}\\\triangle ABC=\triangle A'B'C'\end{array}\right.\).
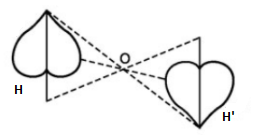
Trong hình trên, hai hình \(H\) và \(H'\) đối xứng với nhau qua điểm \(O\).
Ví dụ:
+) Cho đoạn thẳng \(AB=5cm\) và điểm \(O\). Lấy \(A',B'\) lần lượt đối xứng với \(A,B\) qua \(O\). Khi đó, ta có \(A'B'=AB=5\left(cm\right).\)
+) Cho tam giác \(ABC\) có \(AB=3cm,AC=4cm,BC=5cm\). Vẽ tam giác \(AB'C'\) là hình đối xứng của tam giác \(ABC\) qua điểm \(A\). Khi đó, không cần vẽ hình, ta có thể suy ra \(\Delta ABC=\Delta AB'C'\)
\(\Rightarrow P_{AB'C'}=P_{ABC}=AB+AC+BC=3+4+5=12\left(cm\right).\)
3. Hình có tâm đối xứng
Xét hình bình hành \(ABCD\) có \(O\) là giao điểm hai đường chéo.
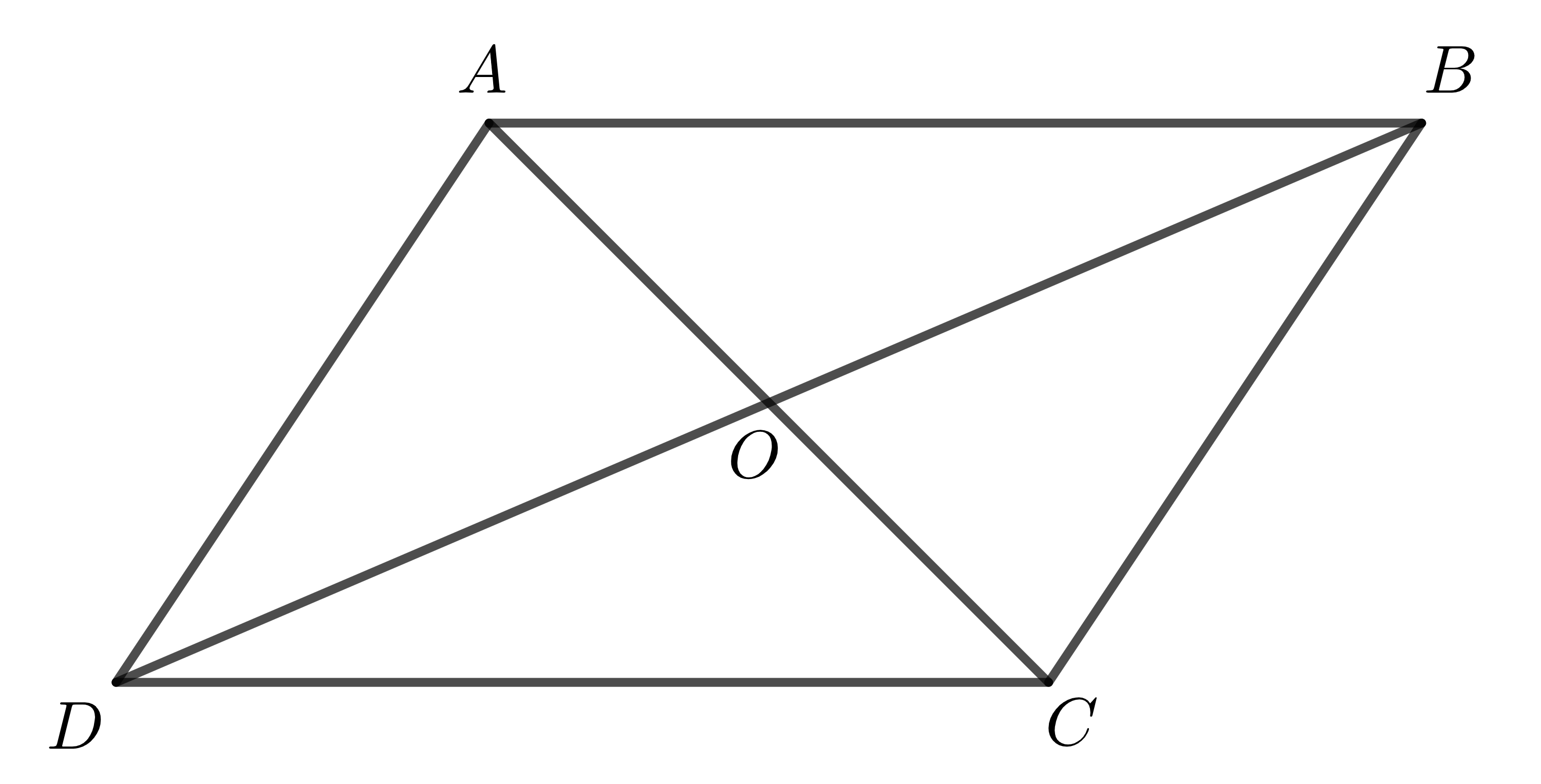
Dễ dàng kiểm tra được: Điểm đối xứng với mỗi điểm thuộc cạnh của hình bình hành \(ABCD\) qua điểm \(O\) cũng thuộc cạnh của hình bình hành.
Ta nói: Điểm \(O\) là tâm đối xứng của hình bình hành \(ABCD\).
Định nghĩa: Điểm \(O\) được gọi là tâm đối xứng của hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua điểm \(O\) cũng thuộc hình \(H\). Khi đó, ta nói \(H\) là hình có tâm đối xứng \(O\).
Từ định nghĩa trên, ta có kết quả:
Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
Ví dụ: Trong bảng chữ cái in hoa có nhiều chữ cái có tâm đối xứng và cũng có nhiều chữ cái không có tâm đối xứng.
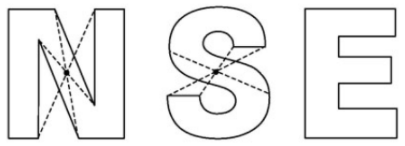
Trong hình trên, các chữ cái N và S có tâm đối xứng; chữ E không có tâm đối xứng.
@606016@