Bài 8: Các trường hợp bằng nhau của tam giác vuông
Nội dung lý thuyết
1. Các trường hợp bằng nhau đã biết của hai tam giác vuông
- Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (theo trường hợp cạnh - góc - cạnh).
Ví dụ: Nếu \(\Delta ABC\) và \(\Delta DEF\) có:
\(\widehat{A}=\widehat{D}=90^0\)
\(AB=DE\)
\(AC=DF\)
thì \(\Delta ABC=\Delta DEF\) (cạnh - góc - cạnh)
Hình vẽ minh hoạ:
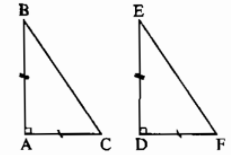
- Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (theo trường hợp góc - cạnh - góc)
Ví dụ: Nếu \(\Delta ABC\) và \(\Delta DEF\) có:
\(\widehat{A}=\widehat{D}=90^0\)
\(AB=DE\)
\(\widehat{B}=\widehat{E}\)
thì \(\Delta ABC=\Delta DEF\) (cạnh góc vuông - góc nhọn kề hay chính là góc - cạnh - góc)
Hình vẽ mình hoạ:
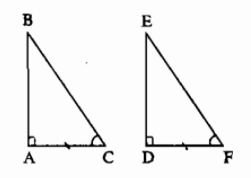
- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (theo trường hợp góc - cạnh - góc)
Ví dụ: Nếu \(\Delta ABC\) và \(\Delta DEF\) có:
\(\widehat{A}=\widehat{D}=90^0\)
\(BC=EF\)
\(\widehat{B}=\widehat{E}\)
thì \(\Delta ABC=\Delta DEF\) (cạnn huyền - góc nhọn hay chính là góc - cạnh - góc)
Hình vẽ minh hoạ:
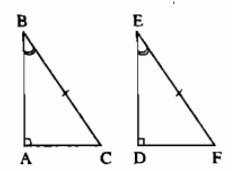
@55975@
2. Trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
Nhờ định lí Py-ta-go, ta có thể chứng minh được trường hợp bằng nhau tiếp theo của hai tam giác vuông:
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Nếu \(\Delta ABC\) và \(\Delta DEF\) có:
\(\widehat{A}=\widehat{D}=90^0\)
\(BC=EF\)
\(AC=DF\)
thì \(\Delta ABC=\Delta DEF\) (cạnh huyền - cạnh góc vuông)
HÌnh vẽ minh hoạ:
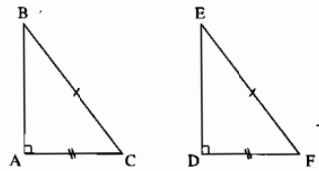
Chứng minh:
Đặt \(BC=EF=a\), \(AC=DF=b\).
Áp dụng định lí Py-ta-go trong tam giác vuông \(ABC\) ta được: \(AB^2+AC^2=BC^2\)
nên \(AB^2=BC^2-AC^2=a^2-b^2\) (1)
Áp dụng định lí Py-ta-go trong tam giác vuông \(DEF\) ta được: \(DE^2+DF^2=EF^2\)
nên \(DE^2=EF^2-DF^2=a^2-b^2\) (2)
Từ (1) và (2) suy ra \(AB^2=DE^2\) \(\Rightarrow\) \(AB=DE\)
Từ đó suy ra \(\Delta ABC=\Delta DEF\) (c.c.c)
@55983@ @1363990@