Bài 7: Hình chóp đều và hình chóp cụt đều
Nội dung lý thuyết
1. Hình chóp
Cho các hình vẽ sau:
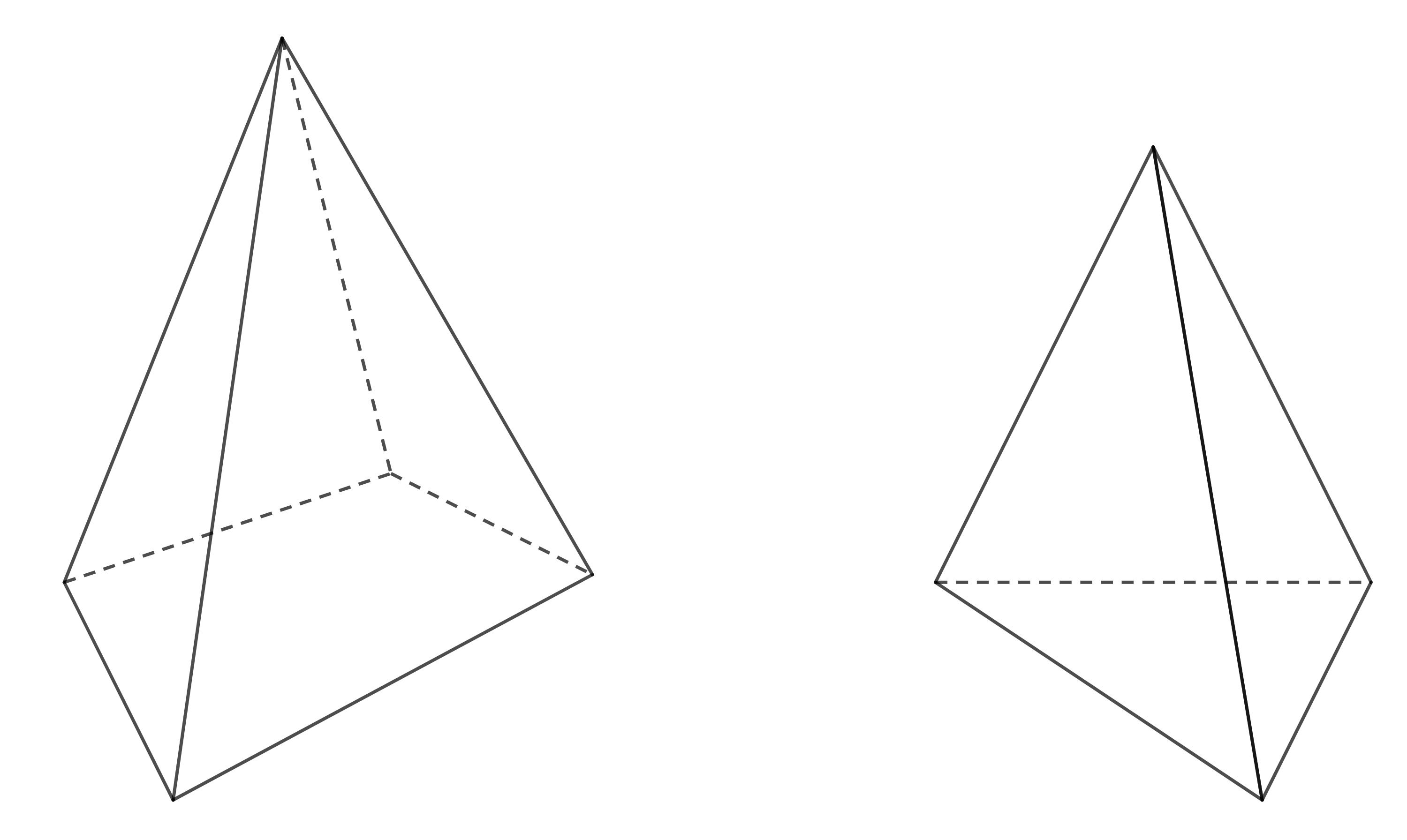
Các hình vẽ trên là các ví dụ về hình chóp.
Ta thấy rằng, chúng đều có mặt đáy là một đa giác còn các mặt bên là các tam giác có chung một đỉnh. Đỉnh chung này gọi là đỉnh của hình chóp.
Đường thẳng đi qua đỉnh \(S\) và vuông góc với mặt phẳng đáy được gọi là đường cao của hình chóp.
Nếu mặt đáy của hình chóp là tứ giác, ta gọi hình chóp đó là hình chóp tứ giác
Nếu mặt đáy của hình chóp là tam giác, ta gọi hình chóp đó là hình chóp tam giác
Nếu mặt đáy của hình chóp là ngũ giác, ta gọi hình chóp đó là hình chóp ngũ giác , v.v...
Ví dụ 1: Ta xét một hình chóp \(S.ABCD\) sau:
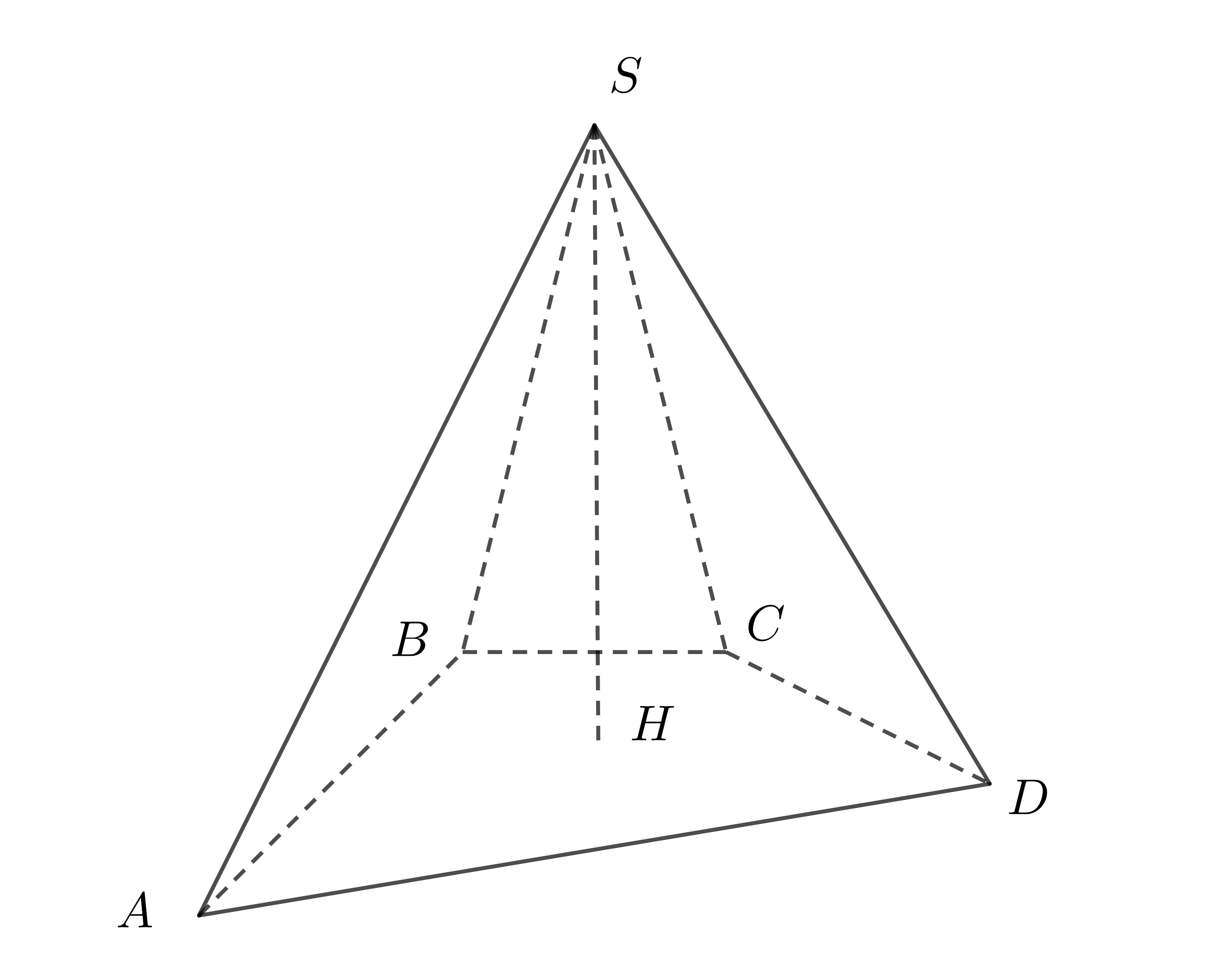
+) \(S\) là đỉnh của hình chóp;
+) Tứ giác \(ABCD\) là đáy của hình chóp, \(AB,BC,CD,DA\) là các cạnh đáy;
+) Các tam giác \(SAB,SBC,SCD,SDA\) là các mặt bên của hình chóp;
+) Các cạnh \(SA,SB,SC,SD\) là các cạnh bên của hình chóp;
+) Đường thẳng đi qua \(S\) và vuông góc với mặt phẳng đáy tại \(H\) tạo thành đoạn thẳng \(SH\) gọi là đường cao của hình chóp.
Ví dụ 2: Xét hình chóp ngũ giác sau:

+) \(S\) là đỉnh của hình chóp;
+) Ngũ giác \(EFGHI\) là mặt đáy của hình chóp; \(EF,FG,GH,HI,IE\) là các cạnh đáy của hình chóp;
+) Các cạnh \(SE,SF,SG,SH,SI\) là các cạnh bên của hình chóp;
+) Các tam giác \(SEF,SFG,SGH,SHI,SIE\) là các mặt bên của hình chóp;
+) \(K\) là chân đường cao kẻ từ \(S\) xuống đáy \(EFGHI\), đoạn thẳng \(SK\) gọi là đường cao của hình chóp.
2. Hình chóp đều
Hình chóp đều là hình chóp có mặt đáy là một đa giác đều, các mặt bên là những tam giác cân bằng nhau có chung đỉnh (là đỉnh của hình chóp).
Ví dụ 1: Hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, các mặt bên \(SAB,SBC,SCD,SDA\) là những tam giác cân bằng nhau, ta nói \(S.ABCD\) là hình chóp tứ giác đều:

Trong hình chóp tứ giác đều \(S.ABCD\) có:
+ Chân đường cao \(H\) là tâm đường tròn đi qua các đỉnh \(A,B,C,D\) của mặt đáy.
+ Đường cao vẽ từ đỉnh \(S\) của mỗi mặt bên của hình chóp đều được gọi là trung đoạn của hình chóp đó.
Ví dụ: Đường cao \(SI\) của tam giác cân \(SCD\) là một trong các trung đoạn của hình chóp.
Ví dụ 2: Hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều, các mặt bên \(SAB,SBC,SCA\) đều là các tam giác cân bằng nhau. Ta nói \(S.ABC\) là hình chóp tam giác đều:
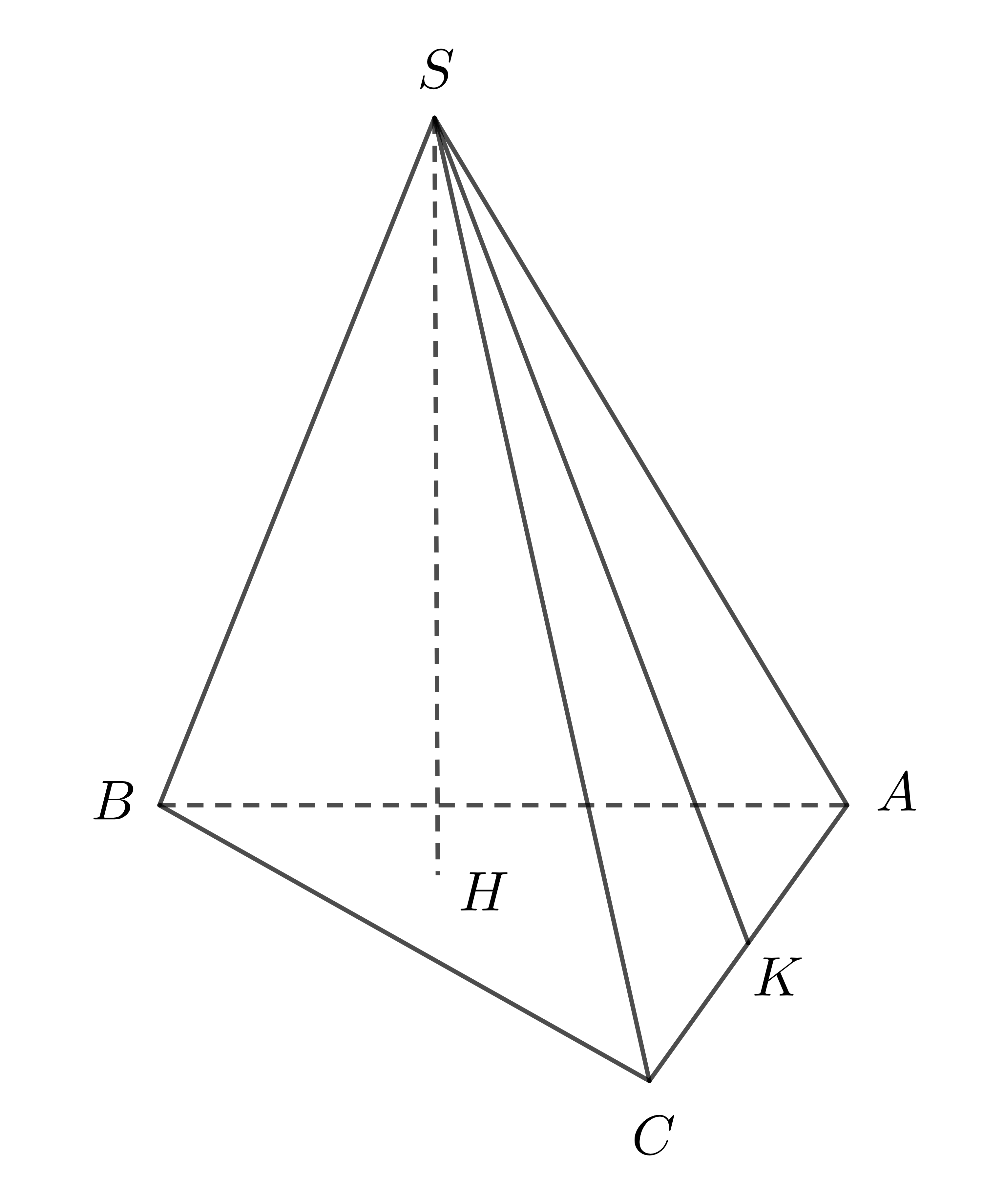
+ \(H\) là chân đường cao kẻ từ đỉnh \(S\) xuống đáy \(ABC\). \(H\) là tâm đường tròn ngoại tiếp tam giác \(ABC\);
+ Đường cao \(SK\) của tam giác \(SAC\) là một trong các trung đoạn của hình chóp.
@1572718@
Ví dụ 3: Cho hình chóp tứ giác đều \(S.ABCD\) có các cạnh đáy bằng \(3cm\), các cạnh bên bằng \(5cm\). Tính độ dài đường cao và trung đoạn của hình chóp?
Giải:

Hình chóp đều \(S.ABCD\) có cạnh đáy \(AB=3cm\), cạnh bên \(SB=5cm\)
Kẻ đường cao \(SH\) và trung đoạn \(SI\) của hình chóp
Do \(ABCD\) là hình vuông nên \(H\) là giao điểm 2 đường chéo
Suy ra \(H\) là trung điềm \(AC,BD\)
\(\Rightarrow HB=\dfrac{1}{2}BD=\dfrac{1}{2}\sqrt{3^2+3^2}=\dfrac{3\sqrt{2}}{2}\)(cm)
Xét \(\Delta SHB\) vuông tại \(H\). Áp dụng định lí Pytago ta có: \(SH^2+HB^2=SB^2\)
\(\Rightarrow SH^2+\left(\dfrac{3\sqrt[]{2}}{2}\right)^2=5^2\)
\(\Rightarrow SH=\sqrt{\dfrac{41}{2}}=\dfrac{\sqrt{82}}{2}\left(cm\right)\)
Do \(\Delta SBC\) cân tại \(S\) mà \(SI\) là đường cao \(\Rightarrow\) \(SI\) đồng thời là trung tuyến \(\Delta SBC\)
\(\Rightarrow\) \(I\) là trung điểm \(BC\)
Xét trong tam giác \(CAB\) có: \(H\) là trung điểm \(AC\), \(I\) là trung điểm \(BC\)
\(\Rightarrow\) \(HI\) là đường trung bình tam giác \(CAB\) \(\Rightarrow HI=\dfrac{1}{2}AB=\dfrac{1}{2}.3=\dfrac{3}{2}\left(cm\right)\)
Áp dụng Pytago trong tam giác vuông \(SHI\) ta có: \(SH^2+HI^2=SI^2\)
\(\Rightarrow SI=\sqrt{SH^2+HI^2}=\sqrt{\dfrac{41}{2}+\dfrac{9}{4}}=\dfrac{\sqrt{91}}{2}\left(cm\right)\)
Vậy độ dài đường cao và trung đoạn của hình chóp lần lượt là \(\dfrac{\sqrt{82}}{2}\left(cm\right)\) và \(\dfrac{\sqrt{91}}{2}\left(cm\right)\).
3. Hình chóp cụt đều
Cắt hình chóp đều bằng một mặt phẳng song song với mặt phẳng đáy. Phần hình chóp nằm giữa mặt phẳng đó và mặt phẳng đáy gọi là hình chóp cụt đều.
Ví dụ 1: Mặt phẳng \(\left(\alpha\right)\) song song với đáy \(ABCD\) và cắt ngang qua hình chóp đều \(S.ABCD\), ta được hình chóp cụt đều:
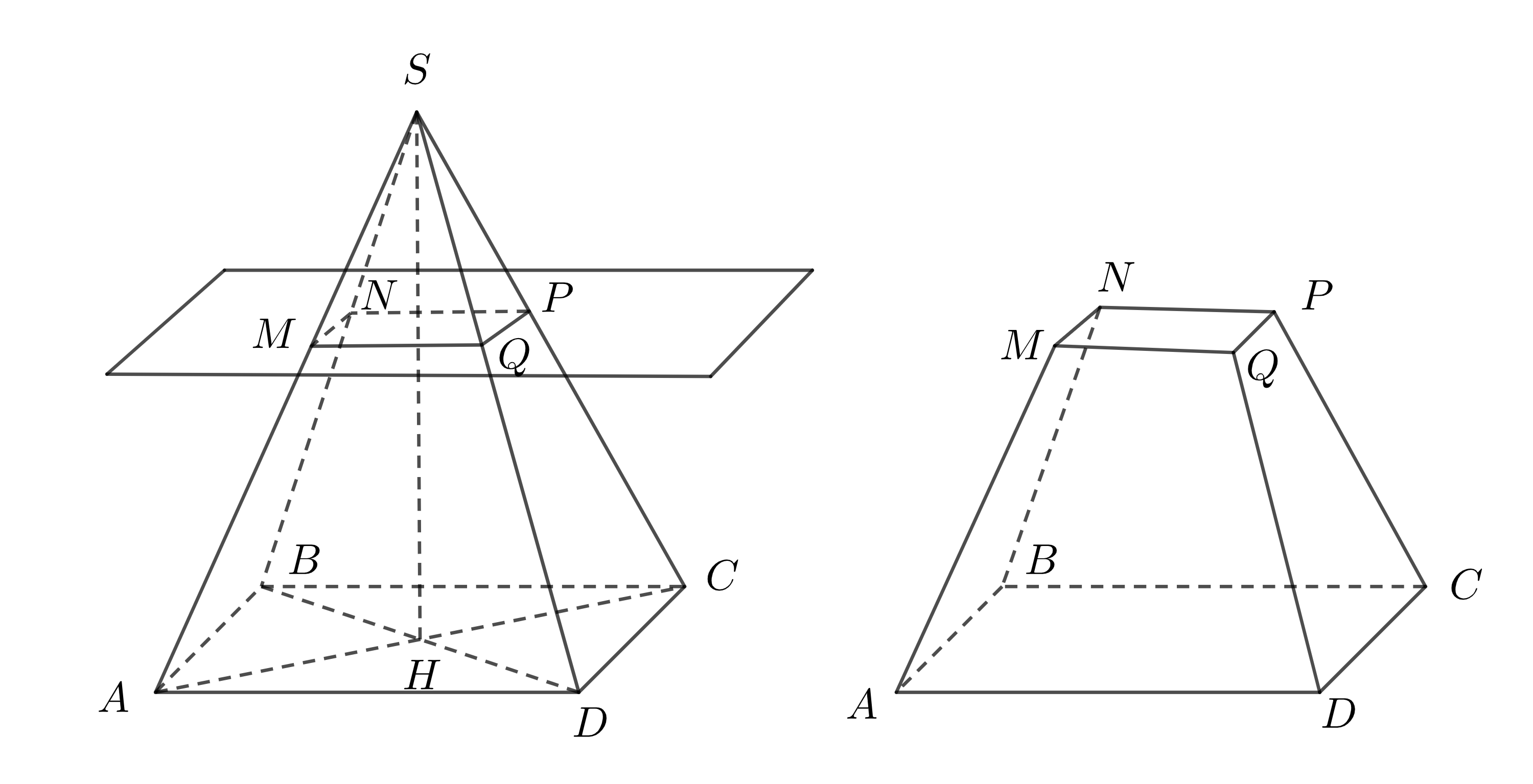
Ví dụ 2: Mặt phẳng \(\left(\beta\right)\) song song với đáy \(BCD\) và cắt ngang qua hình chóp đều \(A.BCD\) ta được hình chóp cụt đều:
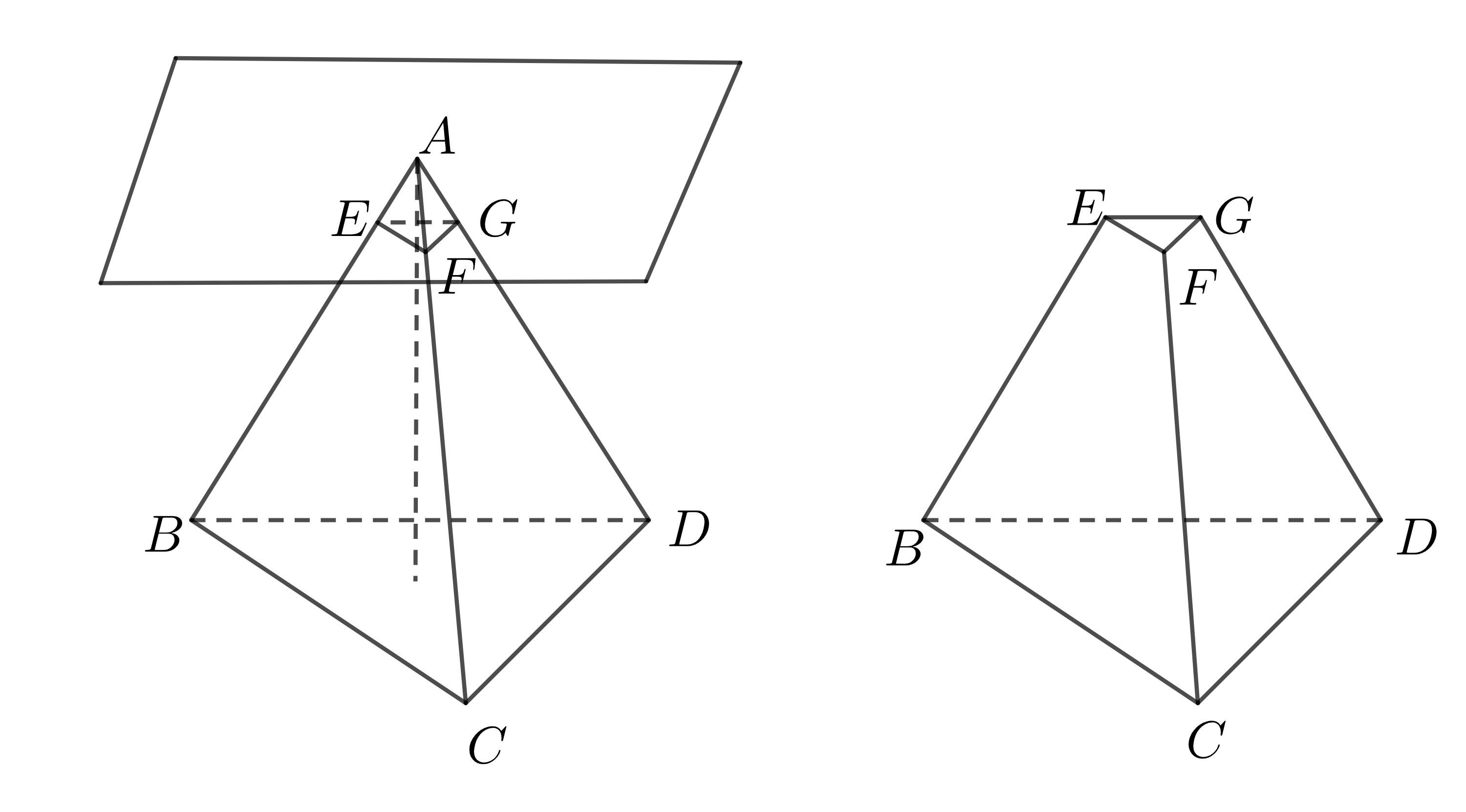
- Nhận xét: Mỗi mặt bên của một hình chóp đều là một hình thang cân.
Ví dụ: Trong hình vẽ trên, \(EFCB\) là một hình thang cân.
@1572794@