Bài 6: Thể tích của hình lăng trụ đứng
Nội dung lý thuyết
1. Công thức tính thể tích
Ở bài trước ta đã biết công thức tính thể tích hình hộp chữ nhật có các kích thước lần lượt là \(a,b,c\) là:
\(V=abc\) hay V = Diện tích đáy x chiều cao
Công thức trên vẫn đúng đối với lăng trụ đứng.
Tổng quát:
Thể tích hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao.
\(V=S.h\)
(\(S\) là diện tích đáy, \(h\) là chiều cao)
@1567239@
2. Các ví dụ
Ví dụ 1: Một lăng trụ đứng có các kích thước được cho như hình vẽ. Tính thể tích của lăng trụ đứng đã cho.

Giải:
Xét đáy tam giác \(ABC\) có: \(AB^2+AC^2=3^2+4^2=25=5^2\)
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại \(A\)
Diện tích đáy \(ABC\) là: \(\dfrac{1}{2}.3.4=6\left(cm^2\right)\)
Thể tích hình lăng trụ là: \(6.7=42\left(cm^3\right)\)
Ví dụ 2: Cho một lăng trụ đứng có đáy là hình thoi \(ABCD\) cạnh bằng \(3cm\) và \(\widehat{BAD}=60^0\). Biết chiều cao lăng trụ là 7cm. Tính thể tích hình lăng trụ đứng trên?
Giải:
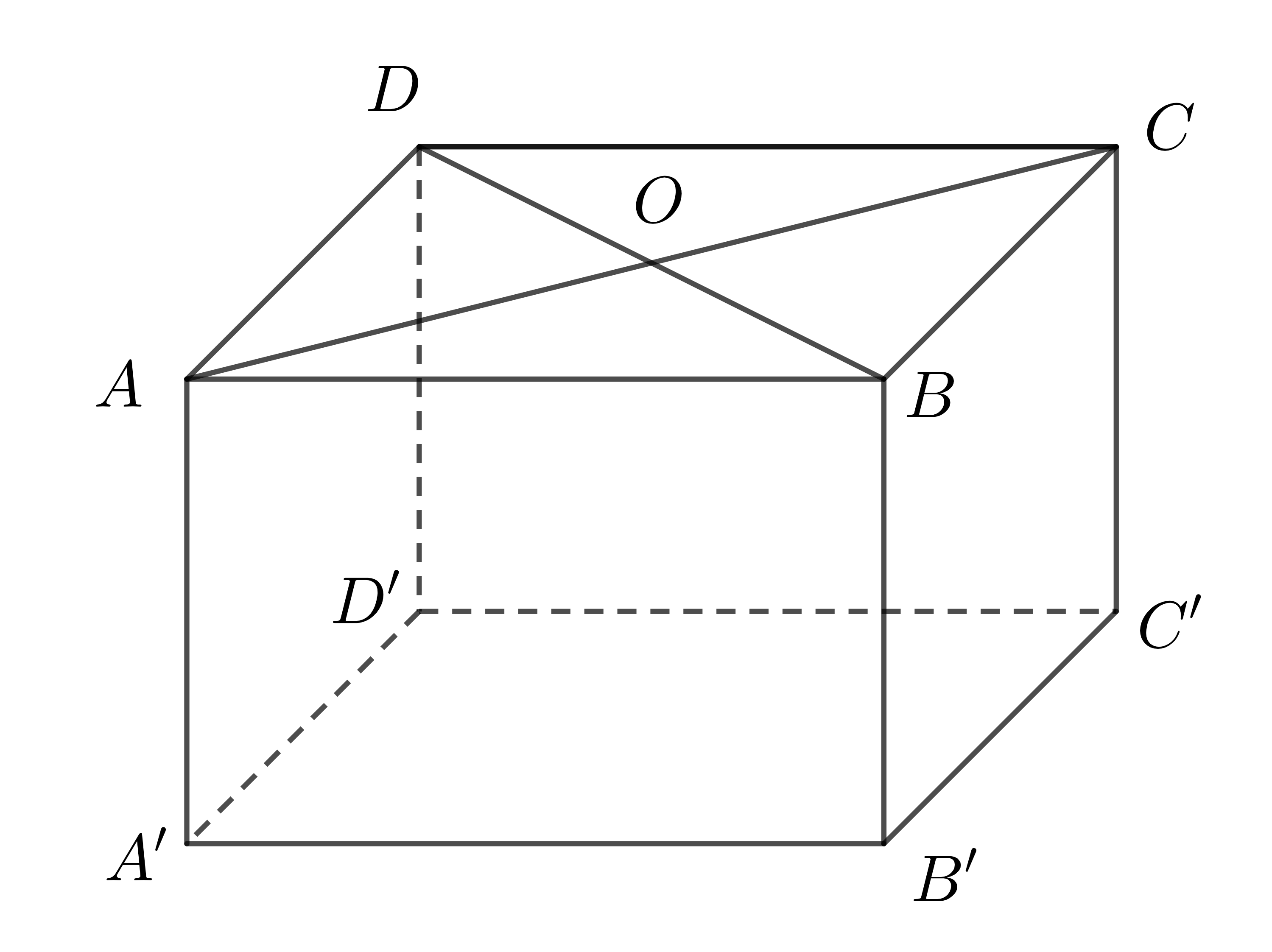
Xét hình thoi \(ABCD\) có \(AB=BC=CD=DA=3cm\)
\(\Rightarrow\Delta BAD\) cân tại \(A\) mà \(\widehat{BAD}=60^0\) \(\Rightarrow\Delta BAD\) đều
\(\Rightarrow BD=3cm\)
Gọi \(O\) là giao điểm 2 đường chéo \(AC,BD\) \(\Rightarrow\) \(O\) là trung điểm mỗi đường và \(AC\perp BD\) tại \(O\)
\(\Rightarrow OB=OD=\dfrac{BD}{2}=1,5\left(cm\right)\)
Xét \(\Delta OAB\) vuông tại \(O\) có \(AB=3cm,OB=1,5cm\)
Áp dụng định lí Py-ta-go ta có: \(OA^2+OB^2=AB^2\)
\(\Rightarrow OA=\sqrt{AB^2-OB^2}=\sqrt{3^2-1,5^2}=\sqrt{6,75}=\dfrac{3\sqrt{3}}{2}\left(cm\right)\)
\(\Rightarrow AC=3\sqrt{3}\left(cm\right)\)
Diện tích hình thoi \(ABCD\) là: \(\dfrac{1}{2}.3.3\sqrt{3}=\dfrac{9\sqrt{3}}{2}\) (cm2)
Thể tích hình lăng trụ là: \(7.\dfrac{9\sqrt{3}}{2}=\dfrac{63\sqrt{3}}{2}\approx54,56\left(cm^3\right)\)
Ví dụ 3: Cho hình lăng trụ đứng ngũ giác có các kích thước như hình vẽ (đơn vị: cm). Tính thể tích lăng trụ đã cho.

Giải:
Hình lăng trụ đã cho gồm một hình hộp chữ nhật và một lăng trụ đứng tam giác có cùng chiều cao.
Hình hộp chữ chật có các kích thước là \(4cm,5cm,7cm\)
Thể tích hình hộp chữ nhật là: \(V_1=4.5.7=140\left(cm^3\right)\)
Hình lăng trụ tam giác có đáy là hình một tam giác có cạnh đáy \(5cm\) và đường cao \(2cm\)
Diện tích đáy tam giác là: \(\dfrac{1}{2}.5.2=5\left(cm^2\right)\)
Thể tích lăng trụ tam giác là: \(V_2=5.7=35\left(cm^3\right)\)
Thể tích của hình lăng trụ đã cho là:
\(V=V_1+V_2=140+35=175\left(cm^3\right)\)
Với bài toán này, ta có thể tính riêng diện tích đáy sao đó lấy diện tích đáy nhân với chiều cao như sau:
Diện tích đáy ngũ giác là: \(4.5+\dfrac{1}{2}.5.2=25\left(cm^2\right)\)
Suy ra thể tích hình lăng trụ là: \(V=25.7=175\left(cm^3\right)\)
@1567368@@1567147@