Bài 6: Đối xứng trục

1. Hai điểm đối xứng qua một đường thẳng

Xét hình vẽ sau:

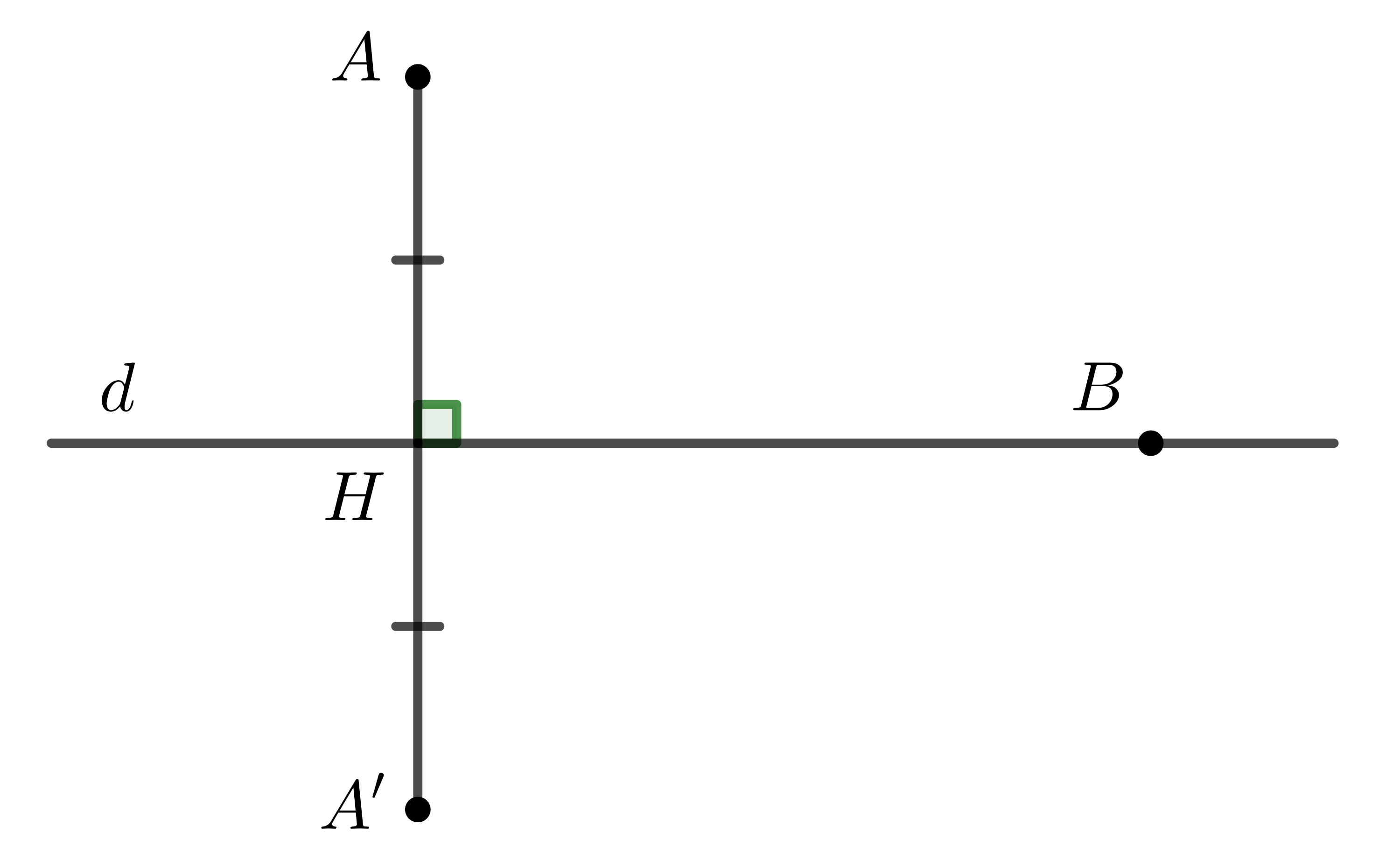
Trong hình vẽ trên, ta thấy đường thẳng \(d\) là đường trung trực của đoạn thẳng \(AA'\). Ta nói: Điểm \(A'\) là điểm đối xứng của \(A\) qua đường thẳng \(d\); Điểm \(A\) là điểm đối xứng của \(A'\) qua đường thẳng \(d\); Hai điểm \(A\) và \(A'\) là hai điểm đối xứng nhau qua đường thẳng \(d\).

Định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của đoạn thẳng nối hai điểm đó.

Quy ước: Điểm \(B\) nằm trên đường thẳng \(d\) thì điểm đối xứng của \(B\) qua đường thẳng \(d\) cũng là điểm \(B\).

2. Hai hình đối xứng qua một đường thẳng

Định nghĩa: Hai hình gọi là đối xứng nhau qua đường thẳng \(d\) nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng \(d\) và ngược lại. 

Ví dụ: 

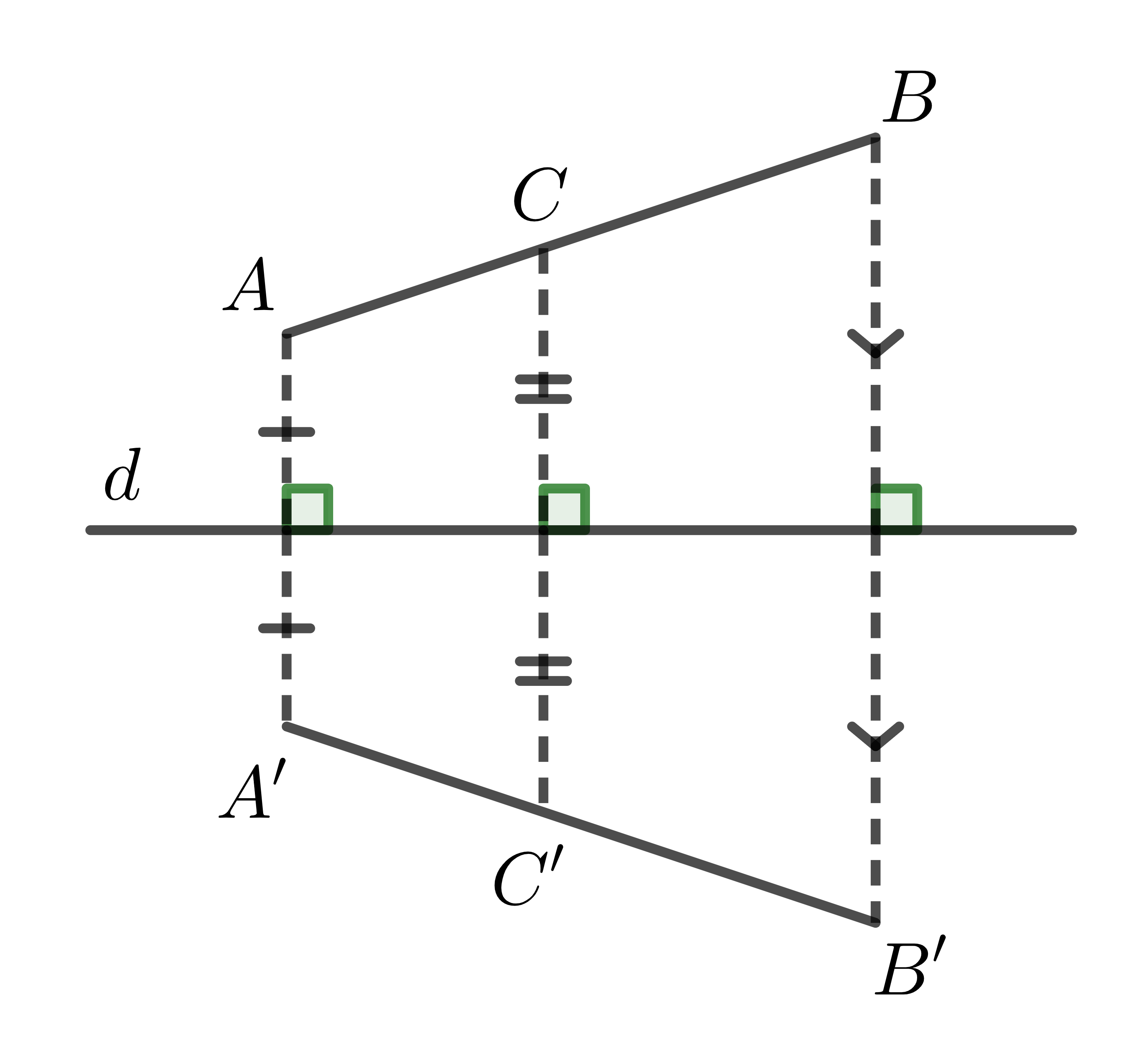
Trong hình vẽ trên: Điểm \(A\) và \(A'\) đối xứng nhau qua đường thẳng \(d\); điểm \(B\) và \(B'\) đối xứng nhau qua đường thẳng \(d\). Lấy điểm \(C\in AB\), điểm đối xứng của \(C\) qua \(d\) là điểm \(C'\in A'B'\).

Ta nói: Hai đoạn thẳng \(AB\) và \(A'B'\) là hai hình đối xứng nhau qua đường thẳng \(d\).

Đường thẳng \(d\) gọi là trục đối xứng của hai hình đó.

Ví dụ: 

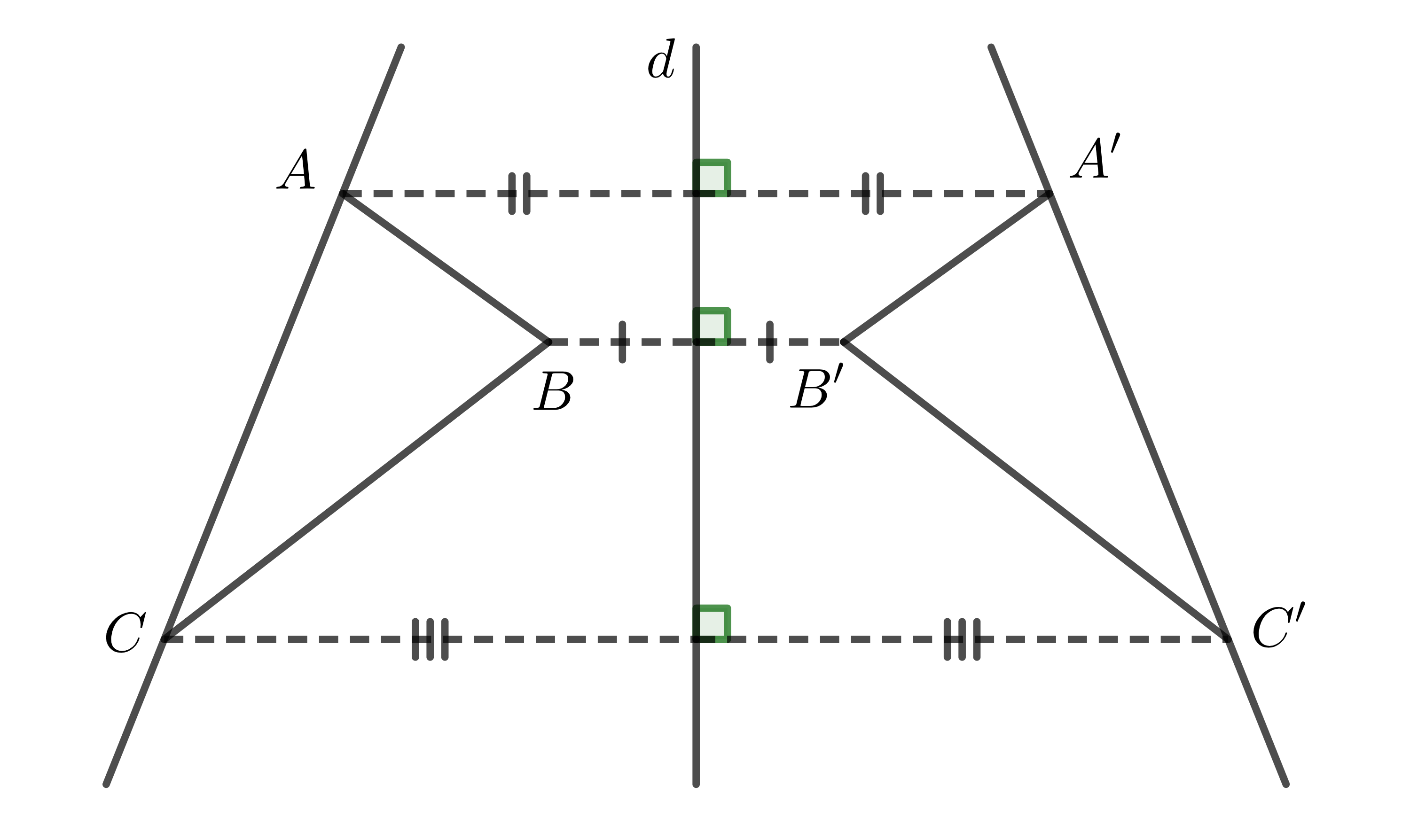
Trong hình vẽ trên, ta có:

• Hai đoạn thẳng \(AB\) và \(A'B'\) đối xứng nhau qua trục \(d\).
• Hai đường thẳng \(AC\) và \(A'C'\) đối xứng nhau qua trục \(d\).
• Hai góc \(ABC\) và \(A'B'C'\) đối xứng nhau qua trục \(d\).
• Hai tam giác \(ABC\) và \(A'B'C'\) đối xứng nhau qua trục \(d\).

Người ta chứng minh được kết quả:

Nếu hai đoạn thẳng (góc, tam giác) đối xứng nhau qua một đường thẳng thì chúng bằng nhau.

Do đó, ta có: \(\left\{{}\begin{matrix}AB=A'B'\\\widehat{ABC}=\widehat{A'B'C'}\\\Delta ABC=\Delta A'B'C'\end{matrix}\right.\).

Ví dụ:

+) Cho đoạn thẳng \(AB=5cm\). Gọi \(A'B'\) là hình đối xứng của \(AB\) qua đường thẳng \(d\) nào đó. Khi đó, ta cũng có \(A'B'=5cm\).

+) Cho tam giác \(ABC\) có chu vi \(P_{ABC}=12cm\). Lấy đối xứng tam giác \(ABC\) qua đường thẳng \(BC\), ta được tam giác \(A'BC\). Khi đó, không cần vẽ hình và tính toán, ta cũng có \(P_{A'BC}=12cm\).

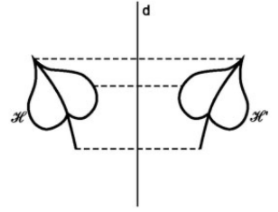
Trong hình trên, hai hình \(H\) và \(H'\) đối xứng với nhau qua đường thẳng \(d\).

3. Hình có trục đối xứng

Ví dụ: Xét tam giác \(ABC\) cân tại \(A\), đường cao \(AH\).

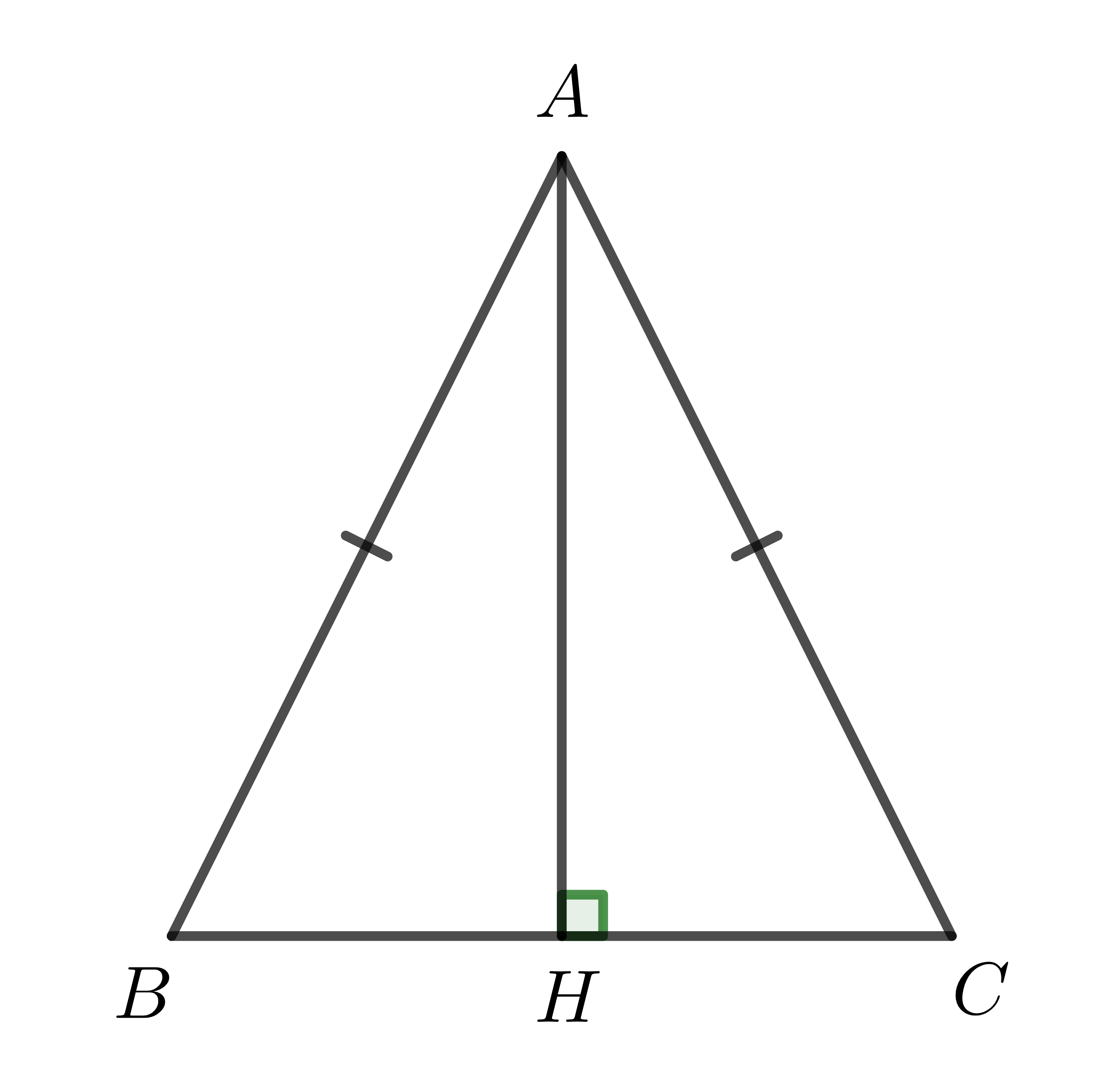
Ta thấy: Điểm đối xứng với mỗi điểm thuộc cạnh của tam giác \(ABC\) qua \(AH\) cũng thuộc cạnh của tam giác \(ABC\). Ta nói \(AH\) là trục đối xứng của tam giác \(ABC\).

Định nghĩa: Đường thẳng \(d\) được gọi là trục đối xứng của hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua đường thẳng \(d\) cũng thuộc hình \(H\).

Ví dụ: Bảng chữ cái in hoa có rất nhiều chữ có trục đối xứng. Chẳng hạn chữ \(A\):

Một số hình quen thuộc ta thường gặp cũng có trục đối xứng:

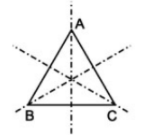
• Tam giác đều \(ABC\) có 3 trục đối xứng (mỗi trục là đường thẳng nối từ đỉnh đến trung điểm cạnh đối diện).
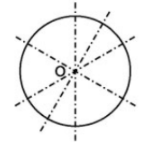
• Hình tròn tâm \(O\) có vô số trục đối xứng (mỗi trục đối xứng chứa một đường kính của nó).
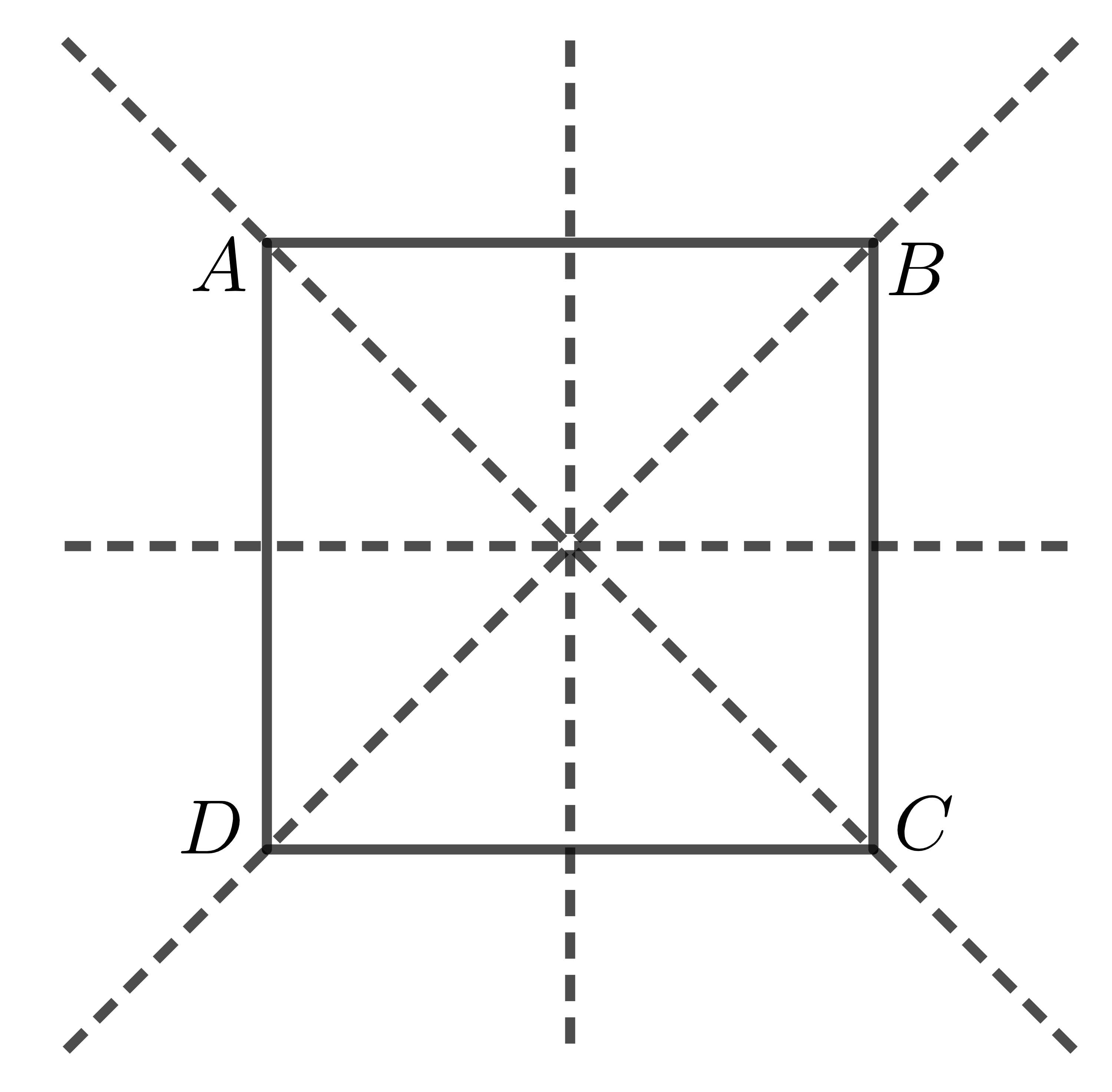
• Hình vuông \(ABCD\) có 4 trục đối xứng (hai đường chéo và hai đường thẳng nối trung điểm hai cạnh đối diện của hình vuông).

Nhận xét: Một hình có thể không có, có thể có một hoặc nhiều trục đối xứng.

Người ta chứng minh được:

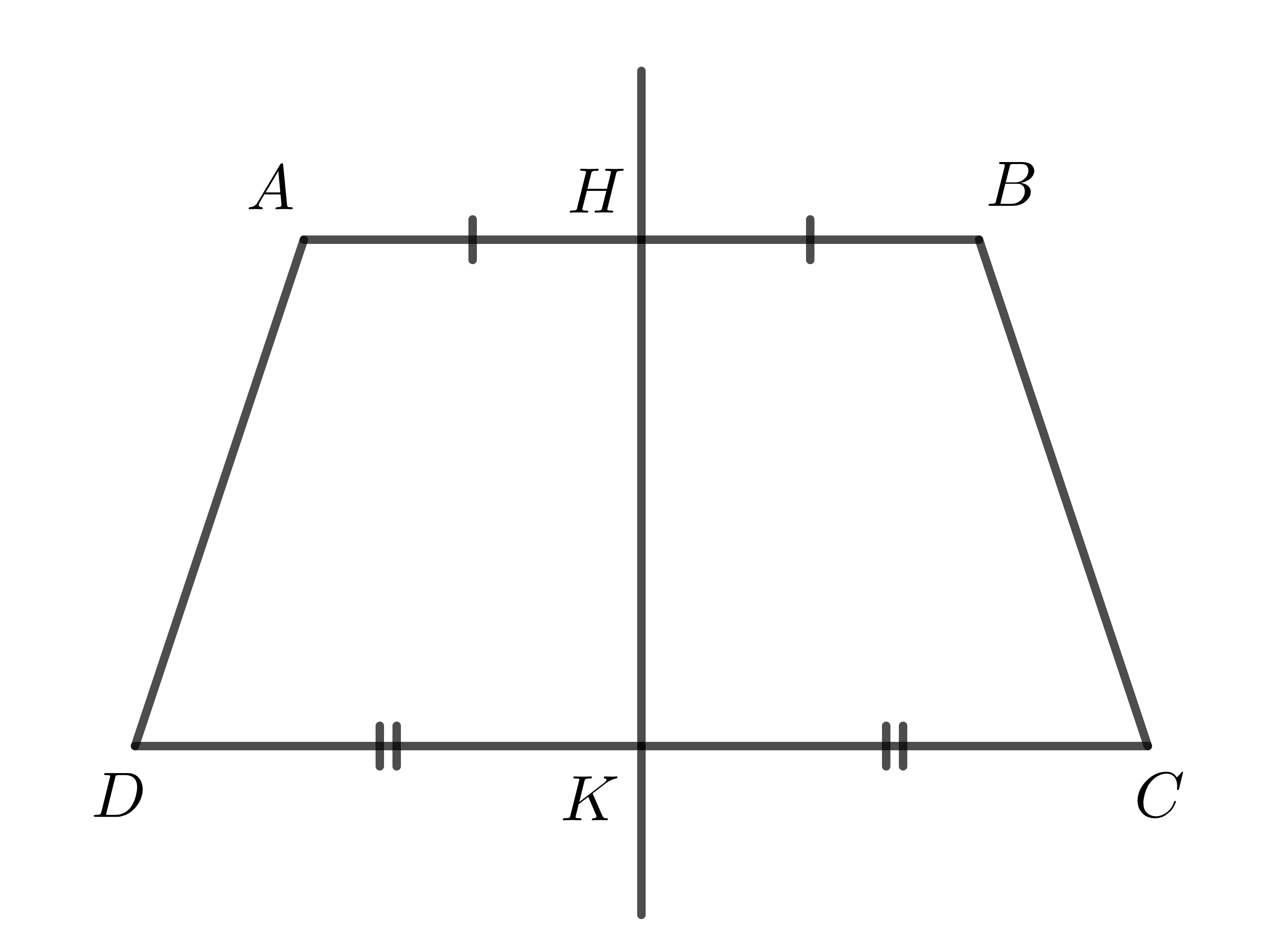
Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.