Bài 5: Hệ số góc của đường thẳng y = ax + b ( a khác 0)
Nội dung lý thuyết
1. Khái niệm hệ số góc của đường thẳng \(y=ax+b\left(a\ne0\right)\)
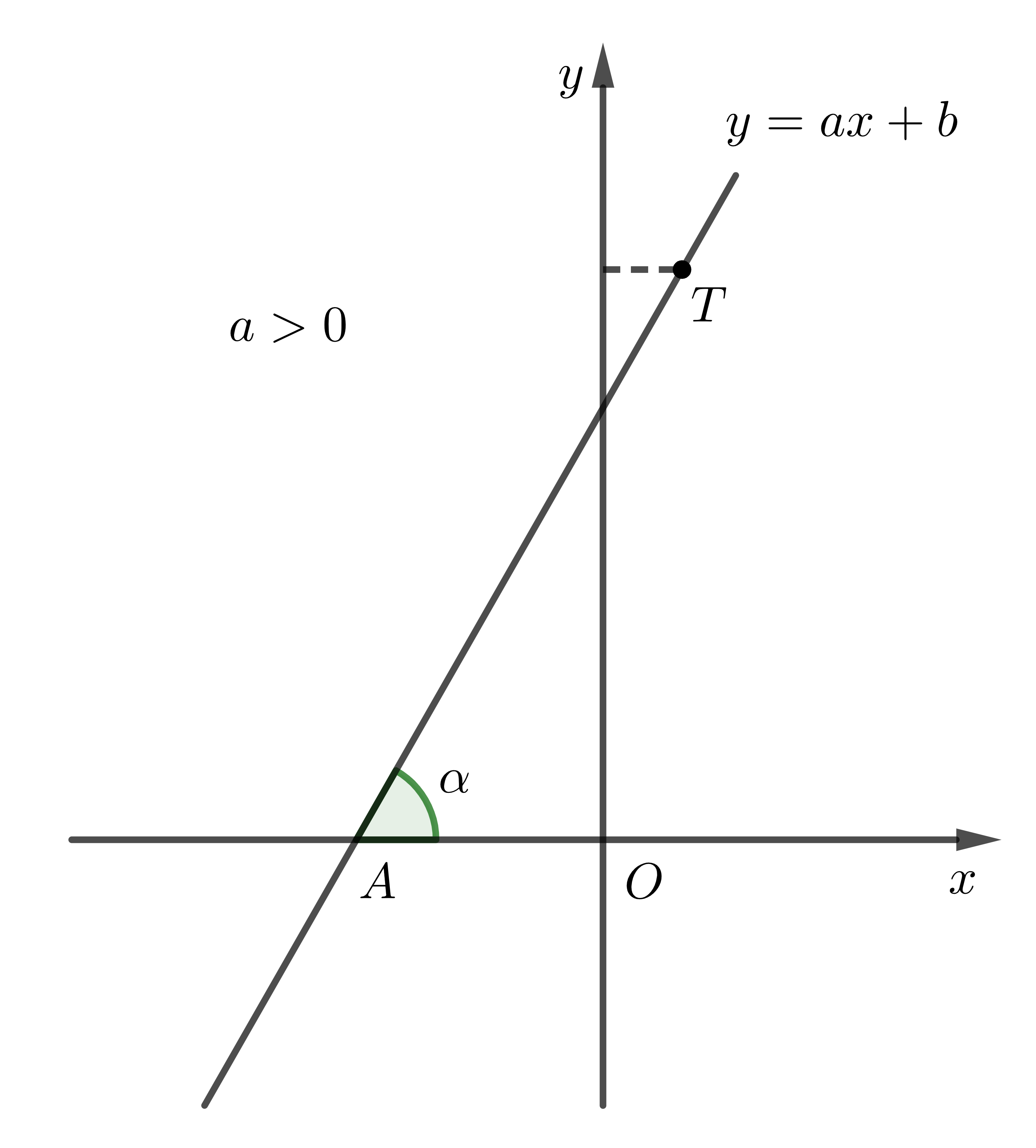
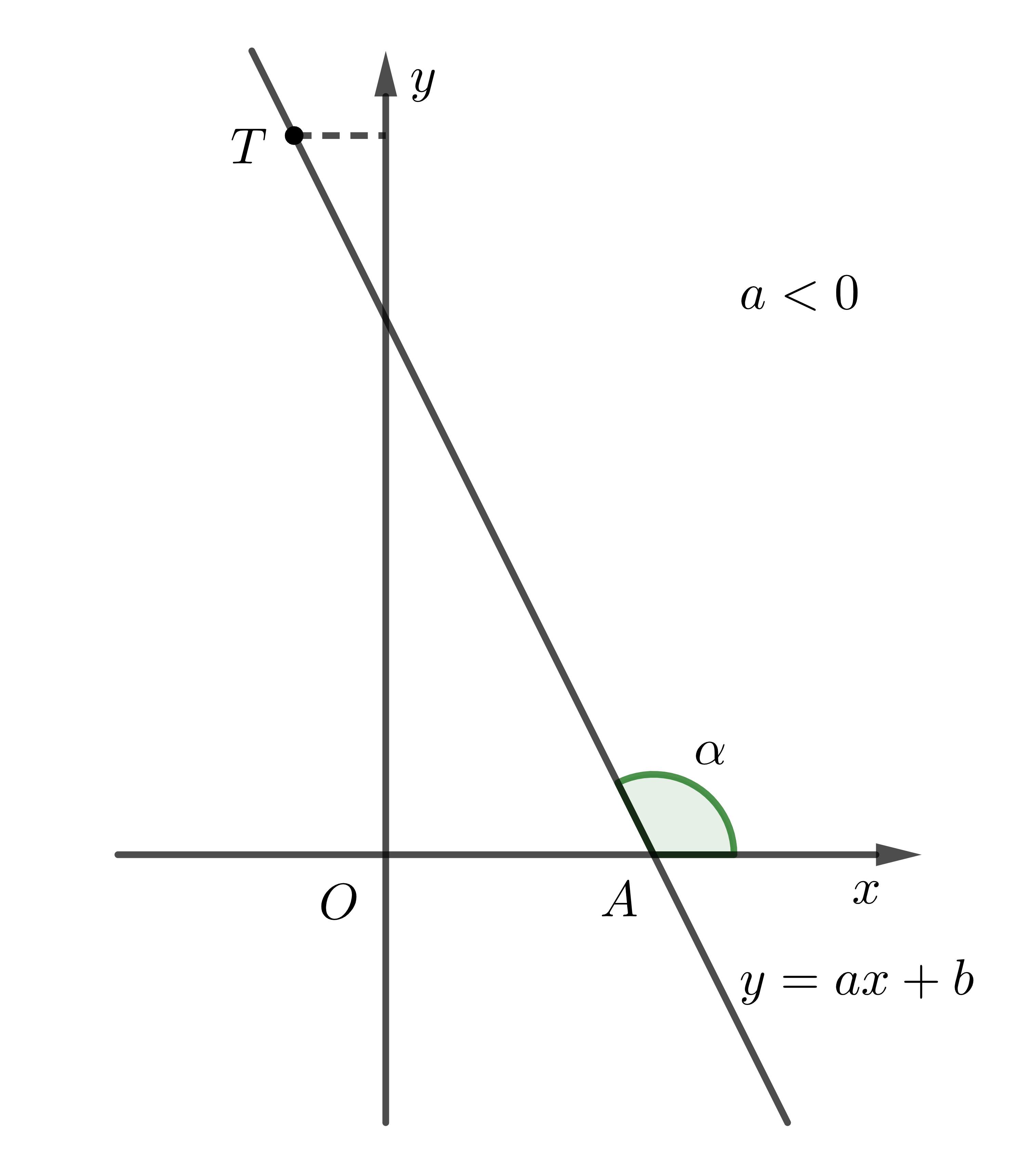
a) Góc tạo bởi đường thẳng \(y=ax+b\) và trục \(Ox\)
Trong mặt phẳng \(Oxy\), gọi \(\alpha\) là góc tạo bởi đường thẳng \(y=ax+b\) và trục \(Ox\).
Khi đó, ta hiểu \(\alpha\) là góc tạo bởi hai tia \(AT\) và \(Ax\), trong đó \(A\) là giao điểm của đường thẳng \(y=ax+b\) và trục \(Ox\), \(T\) là điểm nằm trên đường thẳng \(y=ax+b\) và có tung độ dương.
b) Hệ số góc
Với cách hiểu góc tạo bởi đường thẳng \(y=ax+b\) với trục \(Ox\) như trên, ta thấy:
Các đường thẳng song song với nhau sẽ tạo với trục \(Ox\) các góc bằng nhau.
Suy ra, các đường thẳng có cùng hệ số \(a\) (\(a\) là hệ số của \(x\)) thì tạo với trục \(Ox\) các góc bằng nhau.
@317192@@317340@
Qua quy nạp, ta thu được các kết quả:
- Khi \(a>0\) thì góc tạo bởi đường thẳng \(y=ax+b\) và trục \(Ox\) là góc nhọn. Hệ số \(a\) càng lớn thì góc càng lớn, nhưng vẫn nhỏ hơn \(90^0\).
- Khi \(a< 0\) thì góc tạo bởi đường thẳng \(y=ax+b\) và trục \(Ox\) là góc tù. Hệ số \(a\) càng lớn thì góc càng lớn, nhưng vẫn nhỏ hơn \(180^0\).
Ta gọi \(a\) là hệ số góc của đường thẳng \(y=ax+b\).
@56899@@56900@@317495@
Chú ý: Khi \(b=0\), ta có đường thẳng \(y=ax\). Khi đó ta cũng nói \(a\) là hệ số góc của đường thẳng \(y=ax\).
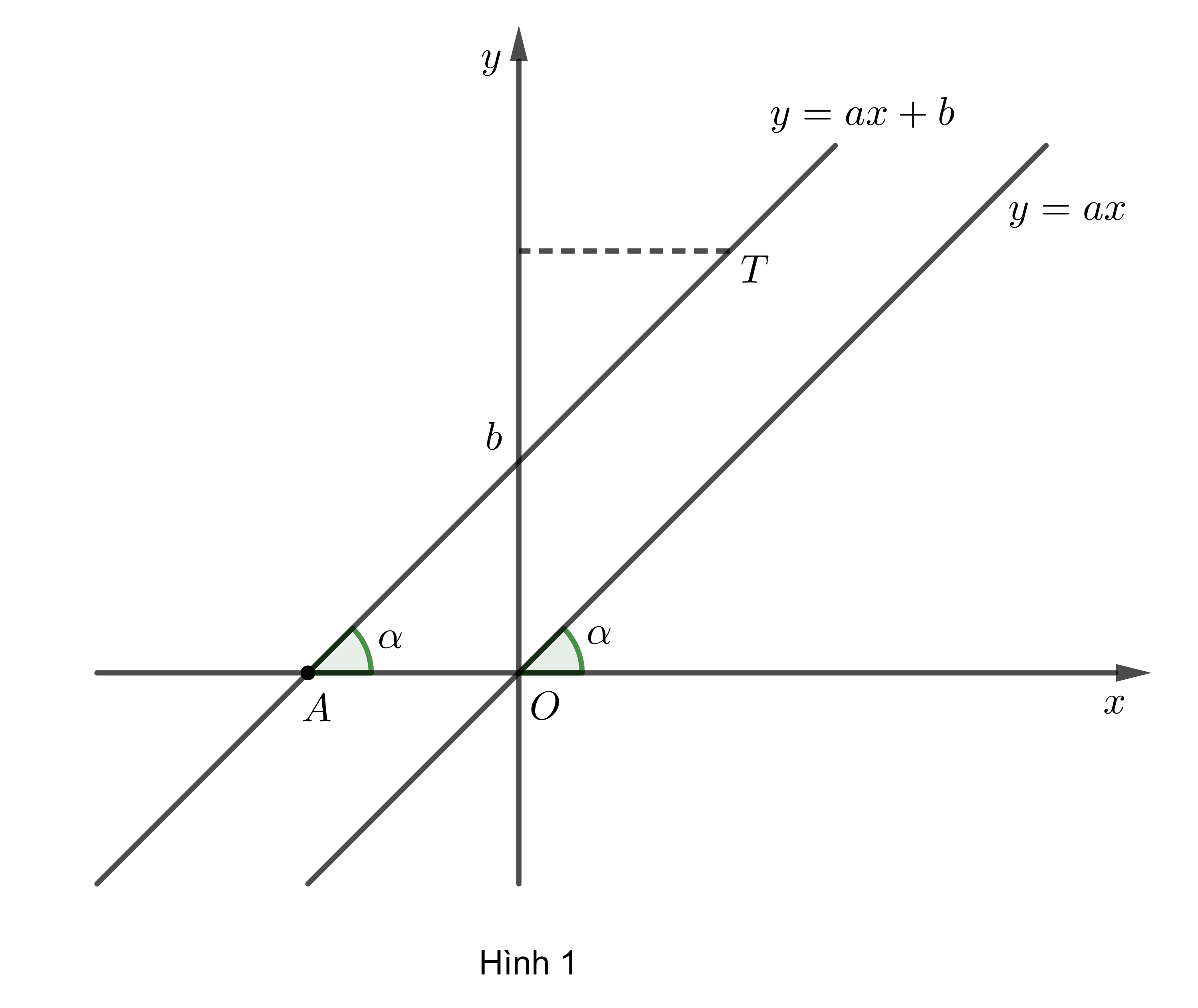
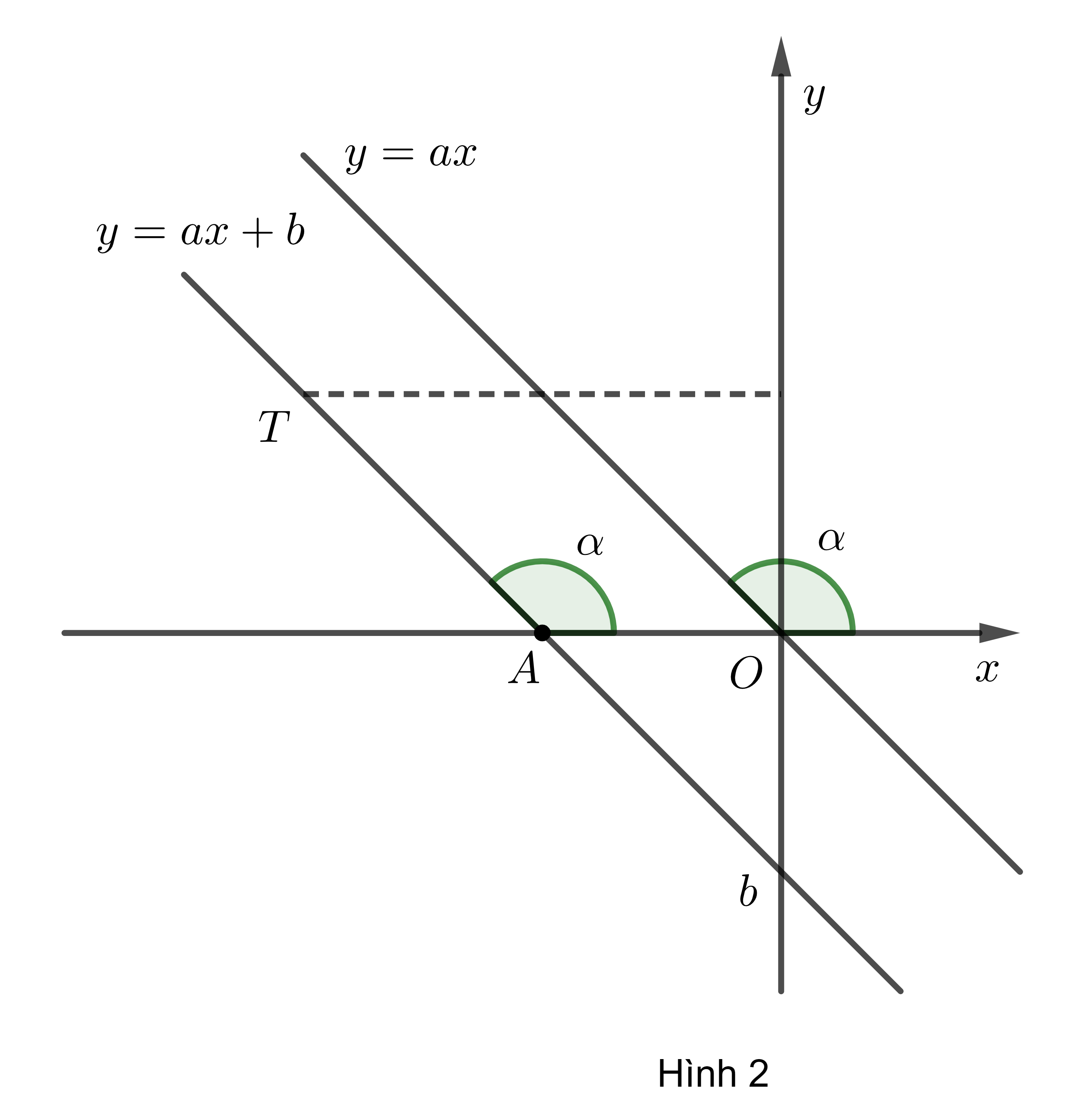
3. Công thức liên hệ giữa \(\alpha\) và hệ số góc \(a\)
Gọi giao điểm của đường thẳng \(y=ax+b\) với trục hoành và trục tung lần lượt là \(A\) và \(B\)
\(\Rightarrow A\left(-\dfrac{b}{a};0\right),B\left(0;b\right)\) \(\Rightarrow OA=\left|\dfrac{b}{a}\right|;OB=\left|b\right|\).
- Khi \(a>0\): Từ hình 1, ta có: \(\tan\alpha=\dfrac{OB}{OA}=\dfrac{\left|b\right|}{\dfrac{\left|b\right|}{a}}=a\).
- Khi \(a< 0\): Từ hình 2, ta có: \(\tan\left(180^0-\alpha\right)=\dfrac{OB}{OA}=\dfrac{\left|b\right|}{\dfrac{\left|b\right|}{-a}}=-a\).
Ta có kết luận:
Với \(\alpha\) là góc tạo bởi đường thẳng \(y=ax+b\left(a\ne0\right)\) và trục hoành:
- Nếu \(a>0\) thì \(a=\tan\alpha\).
- Nếu \(a< 0\) thì \(a=-\tan\left(180^0-\alpha\right)\).
@317125@
Ví dụ:
a) Xét đường thẳng \(y=\sqrt{3}x-1\). Gọi \(\alpha\) là góc tạo bởi đường thẳng với trục hoành. Ta có: \(a=\sqrt{3}>0\) nên \(\alpha\) là góc nhọn và \(\tan\alpha=\sqrt{3}\Rightarrow\alpha=60^0\).
b) Xét đường thẳng \(y=-x+\dfrac{1}{3}\). Gọi \(\beta\) là góc tạo bởi đường thẳng với trục hoành. Ta có: \(a=-1< 0\) nên \(\beta\) là góc tù và \(\tan\left(180^0-\beta\right)=-\left(-1\right)=1\Rightarrow180^0-\beta=45^0\Rightarrow\beta=135^0\).
@56901@@317249@