Bài 3. Phép cộng và phép trừ đa thức

Bài toán mở đầu

Trong buổi sinh hoạt câu lạc bộ Toán học của lớp, hai bạn tính giá trị của hai đa thức P = 2x²y – xy² + 22 và Q = xy² – 2x²y + 23 tại những giá trị cho trước của x và y. Kết quả được ghi lại như bảng bên.

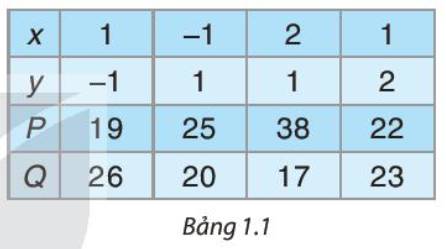
Ban giám khảo cho biết một cột chắc chắn có kết quả sai.

Theo em, làm thế nào để có thể nhanh chóng phát hiện cột đó?

Phép cộng và phép trừ đa thức

Chú ý:

- Phép cộng đa thức cũng có các tính chất giao hoán và kết hợp tương tự như phép cộng các số. 

- Với các đa thức A, B, C tùy ý ta có:

   \( A+B+C = (A+B)+C = A+(B+C)\).

  Nếu  \( A - B=C \) thì \( A - B = C\)

   Ngược lại, nếu \(A=B+C \) thì \(A-B=C\).

Ví dụ 1:

Cho các đa thức \(A=x^2y^2-3xy+3\) và \(B=3x^2y^2+0,5xy-4x+1\)

Hãy tính \(A+B\) và \(A-B\).

Hướng dẫn giải:

\(A+B = (x^2y^2-3xy+3)+(3x^2y^2+0,5xy-4x+1)\) (Viết tổng theo hàng ngang).

\(= x^2y^2-3xy+3+3x^2y^2+0,5xy-4x+1\) (bỏ dấu ngoặc các đa thức).

\(= (x^2y^2+3x^2y^2)+(-3xy+0,5xy)-4x+(3+1)\) (nhóm các đơn thức đồng dạng).

\(=4x^2y^2-2,5xy-4x+4\) (thực hiện phép tính).

\(A-B = (x^2y^2-3xy+3)-(3x^2y^2+0,5xy-4x+1)\) (viết hiệu theo hàng ngang).

\(=x^2y^2-3xy+3-3x^2y^2-0,5xy+4x-1\) (bỏ dấu ngoặc và đổi dấu đa thức B).

\(= (x^2y^2-3x^2y^2)+(-3xy-0,5xy)+4x+(3-1)\) (nhóm các đơn thức đồng dạng).

\(=-2x^2y^2-3,5xy+4x+2\) (thực hiện phép tính).

Ví dụ 2: Trở lại bài toán mở đầu, hãy tính P + Q và nhận xét về đa thức P + Q.

Hướng dẫn giải

Ta có 

\(P+Q=(2x^2y-xy^2+22)+(xy^2-2x^2y+23)\\ =2x^2y-xy^2+22+xy^2-2x^2y+23\\ =(2x^y-2x^2y)-(xy^2-xy^2)+(22+23)\\ =45\)

Đa thức P + Q có giá trị không đổi bằng 45.