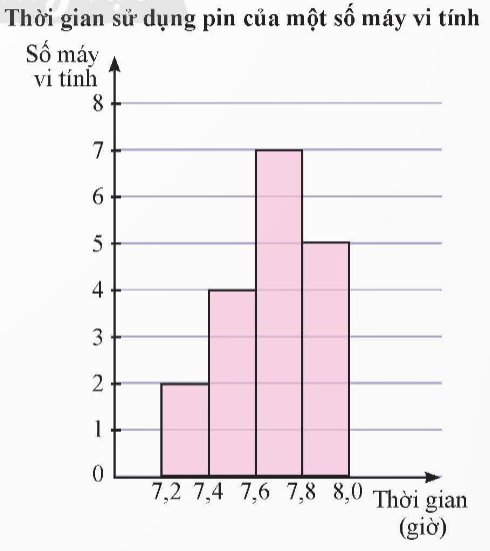
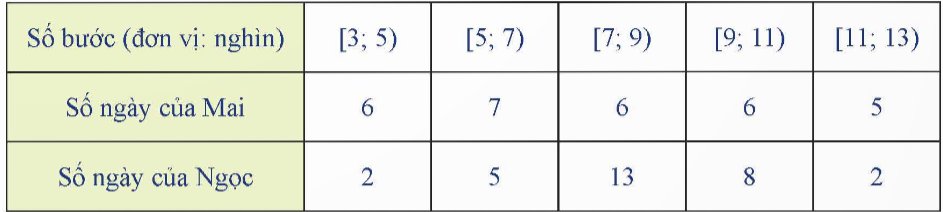
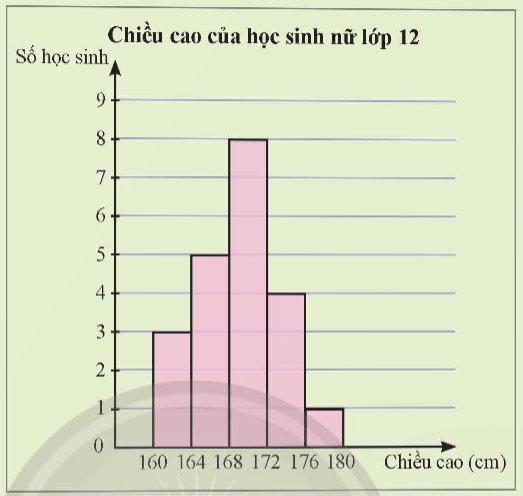
Một giống cây xoan đào được trồng tại hai địa điểm A và B. Người ta thống kê đường kính thân của một số cây xoan đào 5 năm tuổi ở bảng sau:
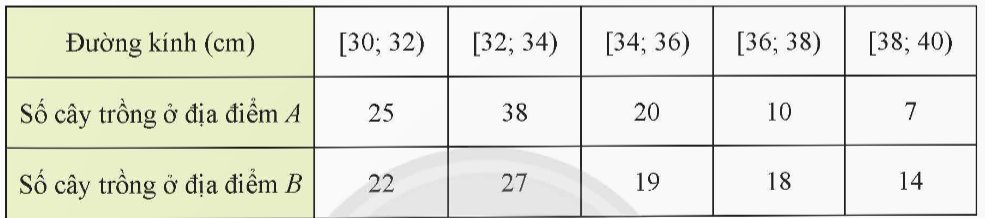
a) Hãy so sánh đường kính trung bình của thân cây xoan đào trồng tại địa điểm A và địa điểm B.
b) Nếu so sánh theo độ lệch chuẩn thì cây trồng tại địa điểm nào có đường kính đồng đều hơn?