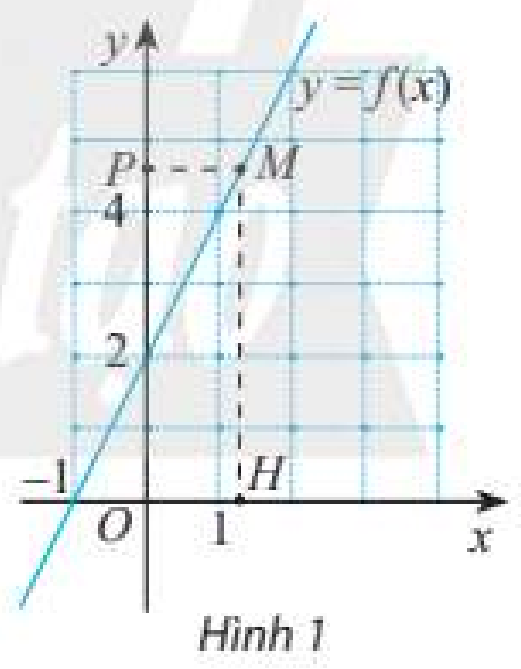
Xét hàm số \(y = f\left( x \right) = \frac{{2{x^2} - 2}}{{x - 1}}\).
a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.
Xét hàm số \(y = f\left( x \right) = \frac{{2{x^2} - 2}}{{x - 1}}\).
a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.

Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right)\);
b) \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}}\).
Thảo luận (1)Hướng dẫn giảia) Đặt \(f\left( x \right) = 2{x^2} - x\).
Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to 3\) khi \(n \to + \infty \). Ta có:
\(\lim f\left( {{x_n}} \right) = \lim \left( {2x_n^2 - {x_n}} \right) = 2.\lim x_n^2 - \lim {x_n} = {2.3^2} - 3 = 15\).
Vậy \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right) = 15\).
b) Đặt \(f\left( x \right) = \frac{{{x^2} + 2x + 1}}{{x + 1}}\).
Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to - 1\) khi \(n \to + \infty \). Ta có:
\(\lim f\left( {{x_n}} \right) = \lim \frac{{x_n^2 + 2{x_n} + 1}}{{{x_n} + 1}} = \lim \frac{{{{\left( {{x_n} + 1} \right)}^2}}}{{{x_n} + 1}} = \lim \left( {{x_n} + 1} \right) = \lim {x_n} + 1 = - 1 + 1 = 0\).
Vậy \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}} = 0\).
(Trả lời bởi Quoc Tran Anh Le)
Cho hai hàm số và \(y = g\left( x \right) = \frac{x}{{x + 1}}\).
a) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thoả mãn \({x_n} \ne - 1\) với mọi \(n\) và \({x_n} \to 1\) khi \(n \to + \infty \). Tìm giới hạn \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right]\).
b) Từ đó, tìm giới hạn \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]\), và so sánh với \(\mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right)\).
Thảo luận (1)Hướng dẫn giảia) \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right] = \lim \left( {2{x_n} + \frac{{{x_n}}}{{{x_n} + 1}}} \right) = 2\lim {x_n} + \lim \frac{{{x_n}}}{{{x_n} + 1}} = 2.1 + \frac{1}{{1 + 1}} = \frac{5}{2}\)
b) Vì \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right] = \frac{5}{2}\) nên \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \frac{5}{2}\) (1).
Ta có: \(\lim {\rm{ }}f\left( {{x_n}} \right) = \lim 2{x_n} = 2\lim {x_n} = 2.1 = 2 \Rightarrow \mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) = 2\)
\(\lim g\left( {{x_n}} \right) = \lim \frac{{{x_n}}}{{{x_n} + 1}} = \lim \frac{{{x_n}}}{{{x_n} + 1}} = \frac{1}{{1 + 1}} = \frac{1}{2} \Rightarrow \mathop {\lim }\limits_{x \to 1} {\rm{ }}g\left( x \right) = \frac{1}{2}\)
Vậy \(\mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 2 + \frac{1}{2} = \frac{5}{2}\) (2).
Từ (1) và (2) suy ra \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - 2} \left( {{x^2} + 5x - 2} \right)\);
b) \(\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}}\).
Thảo luận (1)Hướng dẫn giảia) \(\mathop {\lim }\limits_{x \to - 2} \left( {{x^2} + 5x - 2} \right) = \mathop {\lim }\limits_{x \to - 2} {x^2} + \mathop {\lim }\limits_{x \to - 2} \left( {5x} \right) - \mathop {\lim }\limits_{x \to - 2} 2\)
\( = \mathop {\lim }\limits_{x \to - 2} {x^2} + 5\mathop {\lim }\limits_{x \to - 2} x - \mathop {\lim }\limits_{x \to - 2} 2 = {\left( { - 2} \right)^2} + 5.\left( { - 2} \right) - 2 = - 8\)
b) \(\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to 1} x + \mathop {\lim }\limits_{x \to 1} 1 = 1 + 1 = 2\)
(Trả lời bởi Quoc Tran Anh Le)
Giá cước vận chuyển bưu kiện giữa hai thành phố do một đơn vị cung cấp được cho bởi bảng sau:
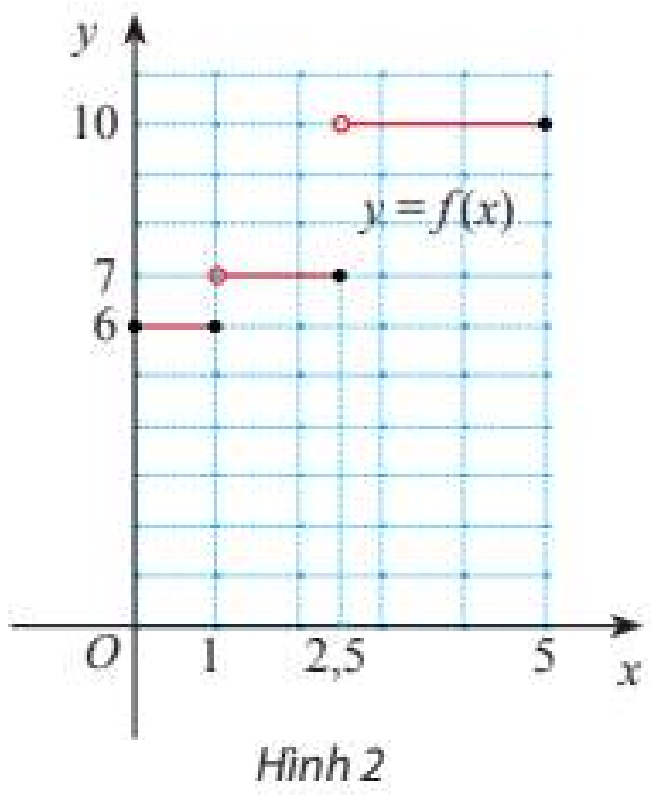
a) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì sao cho \(x \in \left( {1;2,5} \right)\) và \(\lim {x_n} = 1\). Tìm \(\lim f\left( {{x_n}} \right)\).
b) Giả sử \(\left( {{x_n}'} \right)\) là dãy số bất kì sao cho \({x_n}' \in \left( {0;1} \right)\) và \(\lim {x_n}' = 1\). Tìm \(\lim f\left( {{x_n}'} \right)\).
c) Nhận xét về kết quả ở a) và b)
Thảo luận (1)Hướng dẫn giảia) Khi \(x \in \left( {1;2,5} \right)\) thì \(f\left( {{x_n}} \right) = 7\) nên \(\lim f\left( {{x_n}} \right) = \lim 7 = 7\).
b) Khi \({x_n}' \in \left( {0;1} \right)\) thì \(f\left( {{x_n}'} \right) = 6\) nên \(\lim f\left( {{x_n}'} \right) = \lim 6 = 6\).
c) Ta thấy \(\lim {x_n} = \lim {x_n}' = 1\) nhưng \(\lim f\left( {{x_n}} \right) \ne \lim f\left( {{x_n}'} \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{1 - 2x}&{khi\,\,x \le - 1}\\{{x^2} + 2}&{khi\,\,x > - 1}\end{array}} \right.\).
Tìm các giới hạn \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to - {1^ - }} {\rm{ }}f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right)\) (nếu có).
Thảo luận (1)Hướng dẫn giảia) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì, \({x_n} > - 1\) và \({x_n} \to - 1\). Khi đó \(f\left( {{x_n}} \right) = x_n^2 + 2\)
Ta có: \(\lim f\left( {{x_n}} \right) = \lim \left( {x_n^2 + 2} \right) = \lim x_n^2 + \lim 2 = {\left( { - 1} \right)^2} + 2 = 3\)
Vậy \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = 3\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì, \({x_n} < - 1\) và \({x_n} \to - 1\). Khi đó \(f\left( {{x_n}} \right) = 1 - 2{x_n}\).
Ta có: \(\lim f\left( {{x_n}} \right) = \lim \left( {1 - 2{x_n}} \right) = \lim 1 - \lim \left( {2{x_n}} \right) = \lim 1 - 2\lim {x_n} = 1 - 2.\left( { - 1} \right) = 3\)
Vậy \(\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right) = 3\).
b) Vì \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ - }} {\rm{ }}f\left( x \right) = 3\) nên \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = 3\).
(Trả lời bởi Quoc Tran Anh Le)
Cho hàm số \(f\left( x \right) = \frac{1}{x}\) có đồ thị như Hình 3.

a) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng lớn (dần tới \( + \infty \))?
b) Tìm các giá trị còn thiếu trong bảng sau:
x | – 100 000 | – 10 000 | – 1 000 | – 100 | – 10 |
y = f(x) | ? | ? | ? | –0,01 | –0,1 |
Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng bé (dần tới \( - \infty \))?
Thảo luận (1)Hướng dẫn giảia)
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
b)
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).
(Trả lời bởi Quoc Tran Anh Le)
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}}\).
Thảo luận (1)Hướng dẫn giảia) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2}\left( {\frac{1}{{{x^2}}} - 3} \right)}}{{{x^2}\left( {1 + \frac{{2x}}{{{x^2}}}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{1}{{{x^2}}} - 3}}{{1 + \frac{2}{x}}} = \frac{{\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{{x^2}}} - \mathop {\lim }\limits_{x \to + \infty } 3}}{{\mathop {\lim }\limits_{x \to + \infty } 1 + \mathop {\lim }\limits_{x \to + \infty } \frac{2}{x}}} = \frac{{0 - 3}}{{1 + 0}} = - 3\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x\left( {1 + \frac{1}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{1 + \frac{1}{x}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\frac{{\mathop {\lim }\limits_{x \to - \infty } 2}}{{\mathop {\lim }\limits_{x \to - \infty } 1 + \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}}} = 0.\frac{2}{{1 + 0}} = 0\).
(Trả lời bởi Quoc Tran Anh Le)
Một cái hồ đang chứa \(200{m^3}\) nước mặn với nồng độ muối \(10kg/{m^3}\). Người ta ngọt hóa nước trong hồ bằng cách bơm nước ngọt vào hồ với tốc độ \(2{m^3}/\)phút.
a) Viết biểu thức \(C\left( t \right)\) biểu thị nồng độ muối trong hồ sau \(t\) phút kể từ khi bắt đầu bơm.
b) Tìm giới hạn \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right)\) và giải thích ý nghĩa.
Thảo luận (1)Hướng dẫn giảia) Khối lượng muối có trong hồ là: \(200.10 = 2000\left( {kg} \right)\).
Sau \(t\) phút kể từ khi bắt đầu bơm, lượng nước trong hồ là: \(200 + 2t\left( {{m^3}} \right)\).
Nồng độ muối tại thời điểm \(t\) phút kể từ khi bắt đầu bơm là: \(C\left( t \right) = \frac{{2000}}{{200 + 2t}}\left( {kg/{m^3}} \right)\)
b) \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{200 + 2t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{t\left( {\frac{{200}}{t} + 2} \right)}} = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{t}.\mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{\frac{{200}}{t} + 2}}\)
\( = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{t}.\frac{{\mathop {\lim }\limits_{t \to + \infty } 2000}}{{\mathop {\lim }\limits_{t \to + \infty } \frac{{200}}{t} + \mathop {\lim }\limits_{t \to + \infty } 2}} = 0.\frac{{2000}}{{0 + 2}} = 0\)
Ý nghĩa: Khi \(t\) càng lớn thì nồng độ muối càng dần về 0, tức là đến một lúc nào đó nồng độ muối trong hồ không đáng kể, nước trong hồ gần như là nước ngọt.
(Trả lời bởi Quoc Tran Anh Le)
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\) có đồ thị như Hình 4.
x
1,1
1,01
1,001
1,0001
y = f(x)
10
100
?
?
Từ đồ thị và bảng trên, có nhận xét gì về giá trị \(f\left( x \right)\) khi \(x\) dần tới 1 phía bên phải?
b) Tìm các giá trị còn thiếu trong bảng sau:
x | 0,9 | 0,99 | 0,999 | 0,9999 |
y = f(x) | – 10 | – 100 | ? | ? |
Từ đồ thị và bảng trên, có nhận xét gì về giá trị \(f\left( x \right)\) khi \(x\) dần tới 1 phía bên trái?
Thảo luận (1)Hướng dẫn giảia)
Giá trị \(f\left( x \right)\) trở nên rất lớn khi \(x\) dần tới 1 phía bên phải.
b)
Giá trị \(f\left( x \right)\) trở nên rất bé khi \(x\) dần tới 1 phía bên trái.
(Trả lời bởi Quoc Tran Anh Le)