Bài 2: Diện tích hình chữ nhật
Nội dung lý thuyết
Các phiên bản khác1. Khái niệm diện tích đa giác
Ở các lớp dưới, ta đã học số đo của một đoạn thẳng, số đo của một góc. Chẳng hạn: Đoạn thẳng \(AB\) có độ dài \(10cm\), góc \(ABC\) có số đo \(74^0\), ...
Ta cũng làm quen với khái niệm "diện tích". Chẳng hạn: Diện tích sân trường là \(700m^2\), diện tích thửa ruộng là \(20ha\), ...
Định nghĩa:
- Diện tích cũng là một số đo.
- Số đo của phần mặt phẳng giới hạn bởi một đa giác được gọi là diện tích đa giác đó.
Nhận xét: Mỗi đa giác có một diện tích xác định. Diện tích đa giác là một số dương.
Tính chất: Diện tích của đa giác có tính chất sau:
- Do diện tích là một "số" nên nó có đầy đủ các tính chất của số. Ta có thể so sánh các diện tích, hay thực hiện các phép toán với diện tích.
- Hai hình bằng nhau thì có diện tích bằng nhau. Tuy nhiên ta không có chiều ngược lại: Hai hình có diện tích bằng nhau chưa chắc đã là hai hình bằng nhau, chẳng hạn hình chữ nhật A và hình tam giác B có cùng diện tích \(50cm^2\) nhưng chúng không là hai hình bằng nhau.
- Nếu một đa giác được chia thành các đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích các đa giác đó.
- Nếu chọn hình vuông có cạnh bằng \(1cm,1dm,1m,...\) làm đơn vị đo diện tích thì đơn vị diện tích tương ứng là \(1cm^2,1dm^2,1m^2,...\)
Chú ý: Diện tích đa giác \(ABCDE\) được kí hiệu là \(S_{ABCDE}\). Khi không cần phân biệt diện tích các hình với nhau, ta có thể kí hiệu là \(S\).

Chẳng hạn, trong hình trên, ta có: \(S_{ABCDE}=S_{ABC}+S_{ACDE}\).
2. Công thức tính diện tích hình chữ nhật
Ta thừa nhận định lí sau:
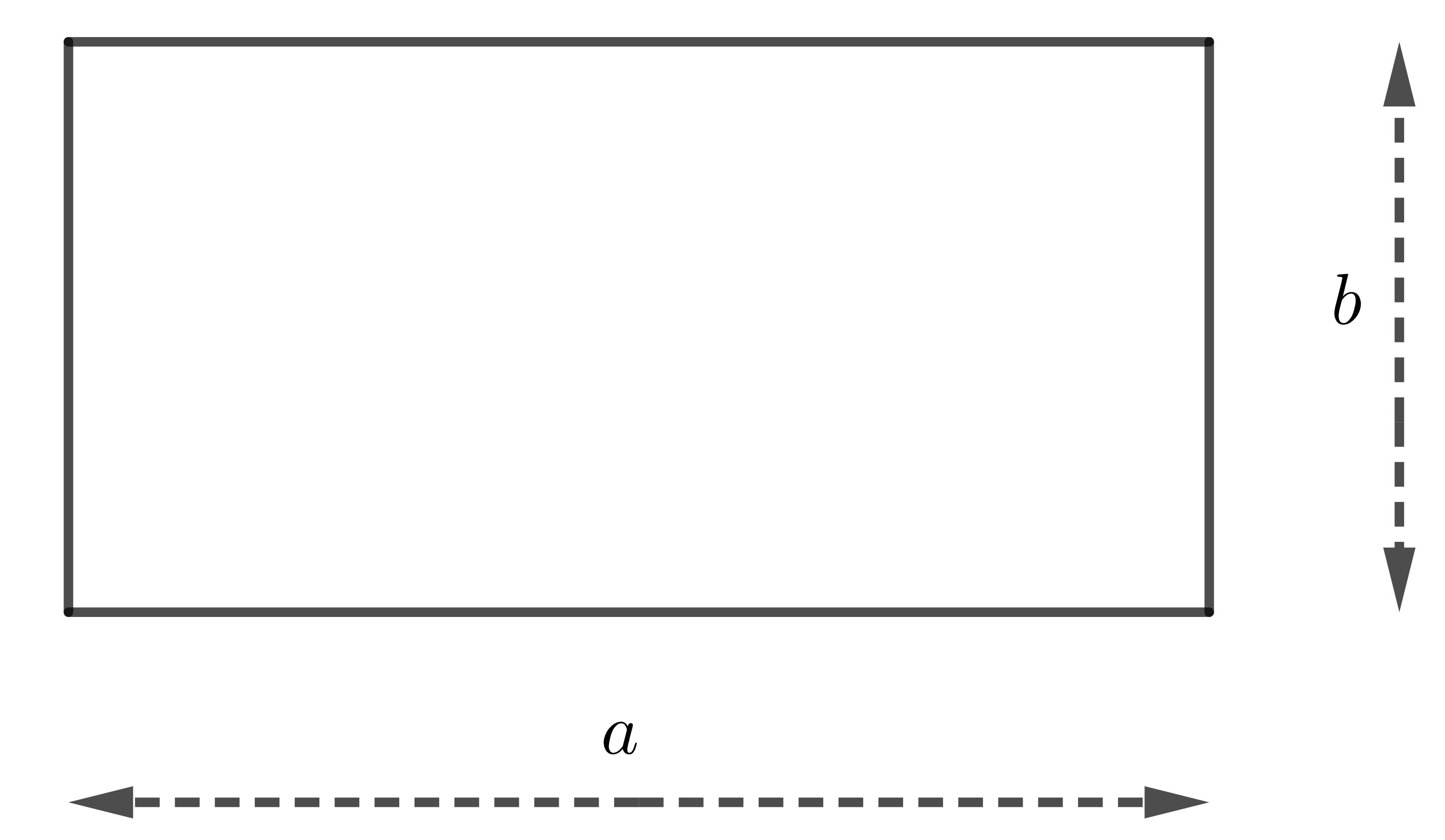
Diện tích hình chữ nhật bằng tích hai kích thước của nó.
\(S=a.b\)
Ví dụ 1: Cho hình chữ nhật có chiều dài \(20cm\), chiều rộng \(6cm\). Khi đó, diện tích hình chữ nhật là: \(S=20.6=120\left(cm^2\right)\).
Ví dụ 2: Khi tăng chiều dài và chiều rộng của một hình chữ nhật lên \(2\) lần thì diện tích của nó thay đổi như thế nào?
Lời giải:
Gọi chiều dài và chiều rộng của hình chữ nhật ban đầu là \(a\) và \(b\)
\(\Rightarrow\) Diện tích hình chữ nhật ban đầu là \(S=a.b\).
Khi tăng mỗi kích thước lên 2 lần, ta được hình chữ nhật mới có các kích thước là \(2a\) và \(2b\)
\(\Rightarrow\) Diện tích hình chữ nhật mới là: \(S'=2a.2b=4a.b=4S\).
Như vậy, khi gấp đôi các kích thước thì diện tích hình chữ nhật tăng lên 4 lần.
@56877@
3. Công thức tính diện tích hình vuông, tam giác vuông
Ta đã biết, hình vuông là hình chữ nhật có hai cạnh kề bằng nhau. Do đó, công thức tính diện tích hình vuông được suy ra trực tiếp từ công thức tính diện tích hình chữ nhật.
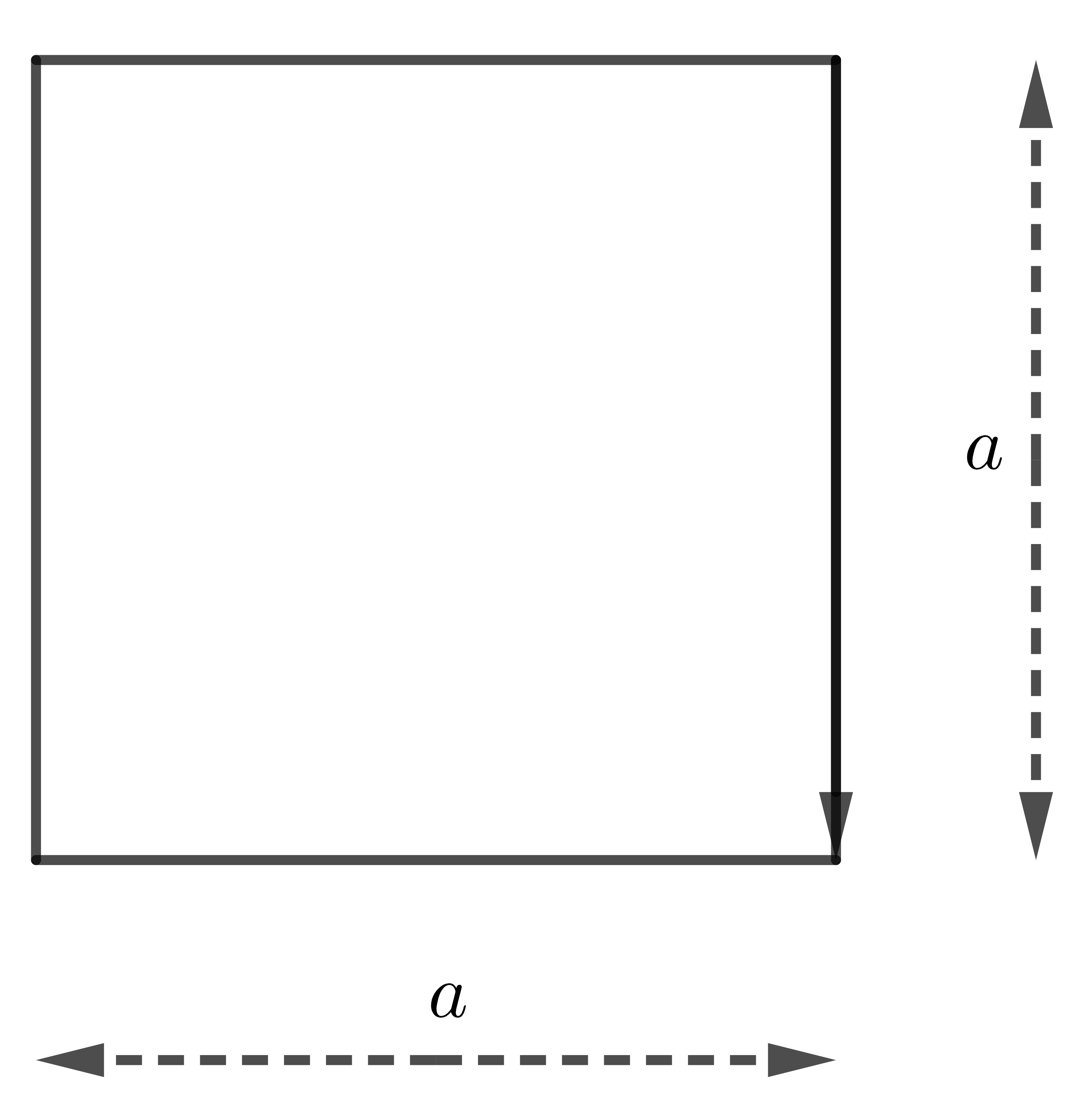
Diện tích hình vuông bằng bình phương cạnh của nó.
\(S=a^2\)
Ví dụ: Khi giảm cạnh hình vuông đi 3 lần thì diện tích của nó thay đổi như thế nào?
Lời giải:
Gọi cạnh hình vuông ban đầu là \(a\) thì diện tích của nó là \(a^2\).
Khi giảm cạnh của nó đi 3 lần, ta được hình vuông mới có cạnh là \(\dfrac{a}{3}\), suy ra diện tích mới là \(\left(\dfrac{a}{3}\right)^2=\dfrac{a^2}{9}\).
Dễ thấy, diện tích mới giảm 9 lần so với diện tích hình vuông ban đầu.
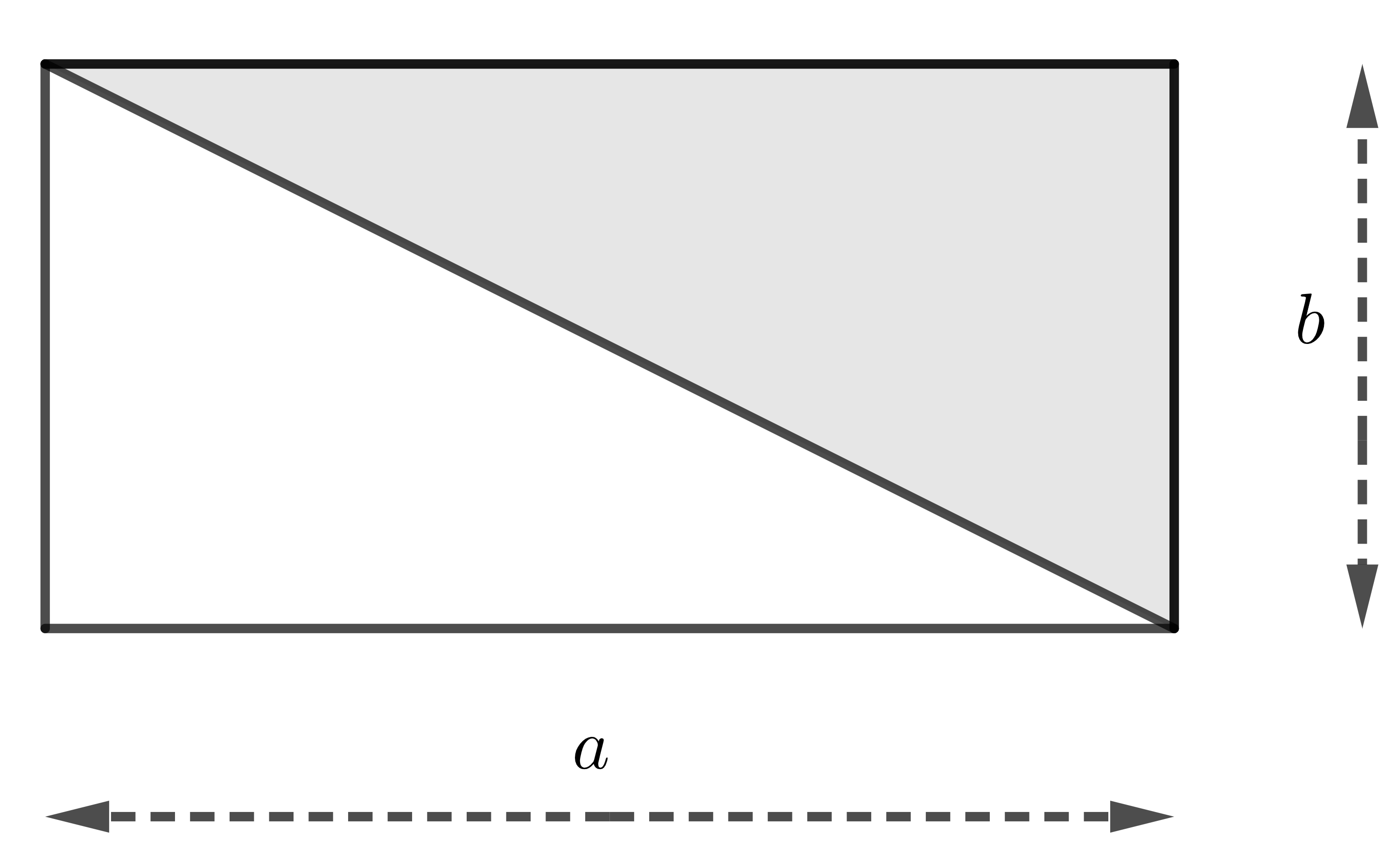
Xét một tam giác vuông đã biết có hai cạnh góc vuông. Dễ thấy tam giác vuông này bằng một nửa hình chữ nhật có hai kích thước là hai cạnh góc vuông đó, do đó ta có định lí:
Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông.
\(S=\dfrac{1}{2}ab\)