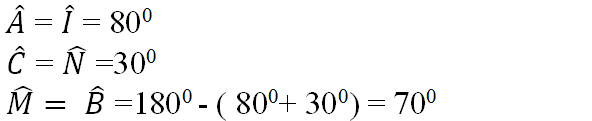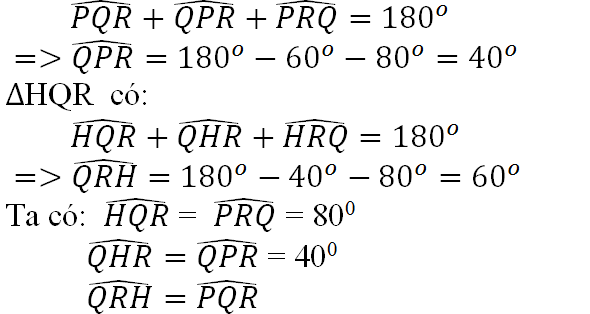Hãy cho một số bài toán ( Ktra1 tiết ) về tam giác cân , các trường hợp bằng nhau của tam giác và lời giải của bài đó

Những câu hỏi liên quan
cho 1 số bài toán (Ktra1 tiết) liên quan đến tam giáccân , các trường hợp bằng nhau của tam giác và lời giải
Cho tam giác ABC, đường cao AH. Trên nửa mặt phẳng bờ AC không chứa điểm B, vẽ tam giác ACD sao cho AD = BC, CD = AB. Chứng minh rằng AB song song với CD và AH vuông góc với AD ( mình mới học hai tam giác bằng nhau theo trường hợp cạnh - cạnh - cạnh thôi, các bạn giải đừng cho tam giác cân, tam giác vuông hay các trường hợp bằng nhau khác của tam giác vào bài giải, thanks)
1. hai tam giác bằng nhau là hai tam giác như thế nào?
2.có mấy trường hợp bằng nhau của hai tam giác? Nêu các trường hợp đó.
3.nêu các trường hợp bằng nhau của hai tam giác vuông.
4.phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh một tam giác là tam giác cân.
5.phát biểu định nghĩa và tính chất tam giác đều.Nêu các cách chưng minh một tam giác là tam giác đều.
6.phát biểu định lí Py-ta-go thuận và đảo.
Đọc tiếp
1. hai tam giác bằng nhau là hai tam giác như thế nào?
2.có mấy trường hợp bằng nhau của hai tam giác? Nêu các trường hợp đó.
3.nêu các trường hợp bằng nhau của hai tam giác vuông.
4.phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh một tam giác là tam giác cân.
5.phát biểu định nghĩa và tính chất tam giác đều.Nêu các cách chưng minh một tam giác là tam giác đều.
6.phát biểu định lí Py-ta-go thuận và đảo.
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
Đúng 0
Bình luận (0)
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
Đúng 0
Bình luận (0)
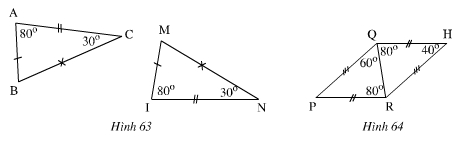
Tìm trong các hình 63, 64 các tam giác bằng nhau ( các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau ). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó. Viết kí hiệu về sự bằng nhau của các tam giác đó .
Hình 63
Ta có:
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
Hình 64 :
ΔPQR có:
Và QH = RP, HR = PQ, QR ( cạnh chung )
Nên ΔHQR = ΔPRQ
Đúng 0
Bình luận (0)
hinh 63
dinh A = dinh I
dinh C = dinh N
dinh B = dinh M
\(\Rightarrow\)tam giac \(ABC=\)tam giac \(IMN\)
hinh 64
dinh P = dinh H
dinh chua goc \(\widehat{PQR}=\)dinh chua goc \(\widehat{QRH}\)
dinh chua goc \(\widehat{PRQ}=\)dinh cua goc \(\widehat{RQH}\)
\(\Rightarrow\)tam giac \(PQR=\)tam giac \(HRQ\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Nhiệm vụ 1: Học thuộc định lý, viết 4 hệ thức về cạnh và góc trong tam giác vuông.Nhiệm vụ 2: Hãy đặt ra một bài toán cho biết cạnh huyền và một góc nhọn của tam giác vuông, yêu cầu tính các cạnh và góc còn lại của tam giác vuông ấy.Nhiệm vụ 3: Hãy đặt ra một bài toán cho biết 2 cạnh của tam giác vuông, yêu cầu tính các cạnh và góc còn lại của tam giác vuông ấy. Nhiệm vụ 4: Tìm hiểu thế nào là giải tam giác vuông?
Đọc tiếp
Nhiệm vụ 1: Học thuộc định lý, viết 4 hệ thức về cạnh và góc trong tam giác vuông.
Nhiệm vụ 2: Hãy đặt ra một bài toán cho biết cạnh huyền và một góc nhọn của tam giác vuông, yêu cầu tính các cạnh và góc còn lại của tam giác vuông ấy.
Nhiệm vụ 3: Hãy đặt ra một bài toán cho biết 2 cạnh của tam giác vuông, yêu cầu tính các cạnh và góc còn lại của tam giác vuông ấy. Nhiệm vụ 4: Tìm hiểu thế nào là giải tam giác vuông?
bài 1 : Cho Δ DEF = Δ MNP . Biết EF + FD = 10cm ,
NP - MP = 2cm, DE = 3cm . Tính các cạnh của mỗi tam giác
bài 2 : Cho 2 tam giác bằng nhau :Δ ABC và 1 tam giác có 3 đỉnh là M,N,P . Hãy viết kí hiệu về sự bằng nhau giữa hai tam giác trong mỗi trường hợp sau , biết :
a) ^A = ^N , ^B = ^M
b) AB= PN, BC= NM
giúp mình với ạ
1:
ΔDEF=ΔMNP
=>DE=MN; EF=NP; DF=MP
EF+FD=10; NP-MP=2; DE=3
=>MN=3cm; EF-DF=2 và EF+FD=10
=>EF=(10+2)/2=6cm và DF=6-2=4cm
EF=NP=6cm; DF=MP=4cm
2:
a: ΔABC=ΔNMP
b: ΔABC=ΔPNM
Đúng 1
Bình luận (0)
Bài 1
Do ∆DEF = ∆MNP
⇒ DE = MN; DF = MP; EF = NP
Do NP - MP = 2 (cm)
⇒ EF - FD = 2 (cm)
Lại có
EF + FD = 10 (cm)
⇒ EF = (10 + 2) : 2 = 6 (cm)
⇒ FD = 10 - 6 = 4 (cm)
Vậy độ dài các cạnh của mỗi tam giác là:
EF = NP = 6 cm
FD = MP = 4 cm
DE = MN = 3 cm
Đúng 2
Bình luận (0)
Bài tập : Cho hai tam giác bằng nhau : tam giác ABC và một tam giác có ba đỉnh là D , E , F . Hãy viết các kí hiệu về sự bằng nhau của hai tam giác đó , biết rằng :
a. A = F , B = E
b. AB = ED , AC = FD
bài 45 của luyện tập về ba trường hợp bằng nhau của tam giác trong sgk toán lp 7 tập 1 trang125
Đọc đề đi mình giải cho. Nhớ tick cho mình trước nhé
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC và một tam giác có ba đỉnh H, I, K viết sự bằng nhau của hai tam giác trong các trường hợp sau:
a) 𝐴̂=𝐼̂ và AB = HI
b) AB = HK và BC = IK.