Cho tam giác ABC các trung tuyến BM;CN cắt nhau tại G gọi P là điểm đối xứng của M qua G ;gọi Q là điểm đối xứng của N qua G
tứ giác MNPQ la hình gì ?
NẾU tam giác ABC cân ở A thì tứ giác MNPQ là hình gì ?vì sao
Cho tam giác ABC cân tại A , các đường trung tuyến BM và CN cắt nhau tại G
Chứng minh tam giác ABC = tam giác ACN , từ đó suy ra BM=CN
Xét ΔABM và ΔACN có
AB=AC
góc BAM chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
Mình xin phép sửa đề:
Cho tam giác ABC cân tại A , các đường trung tuyến BM và CN cắt nhau tại G
Chứng minh tam giác ABN = tam giác ACN , từ đó suy ra BM=CN
`------`
\(\text{GT | AB = AC, }\widehat{\text{B}}=\widehat{\text{C}}\)
\(\text{CM | BM = CN}\)
\(\text{BM là đường trung tuyến}\)
`->`\(\text{MA = MC (1)}\)
\(\text{CN là đường trung tuyến}\)
`->`\(\text{NA = NB (2)}\)
`\Delta ABC` cân tại A
`->`\(\widehat{\text{B}}=\widehat{\text{C}}\text{, AB = AC (3)}\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
`->`\(\text{NA = NB = MA = MC}\)
Xét `\Delta ABM` và `\Delta ACN`:
\(\left\{{}\begin{matrix}\text{BM = CN}\\\widehat{\text{B}}=\widehat{\text{C}}\\\text{BC chung}\end{matrix}\right.\)
`=> \Delta ABM = \Delta ACN (c-g-c)`
`->`\(\text{BM = CN (2 cạnh tương ứng).}\)
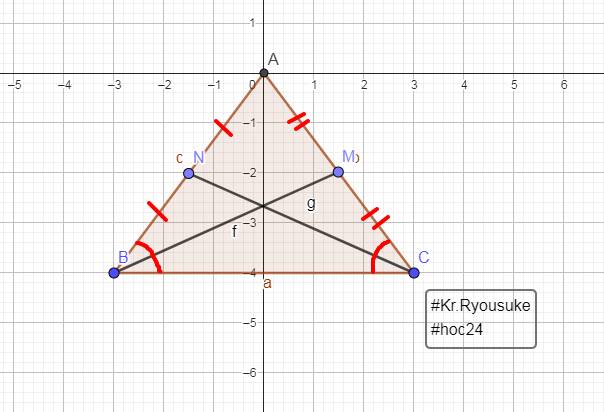
Cho tam giác ABC, các đường trung tuyến BM và CN cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của GC
cho tam giác ABC, các đường trung tuyến BM và CN cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của GC.
a,cho BC=10cm.Tính MN
b, Chứng minh MNHK là hình bình hành
a: Xét ΔABC có
M là trung điểm của AC
N là trung điểm của AB
Do đó: MN là đường trung bình của ΔABC
Suy ra: \(MN=\dfrac{BC}{2}=5\left(cm\right)\)
Cho tam giác ABC, các đường trung tuyến BM, CN. Biết góc ABM= góc ACN. CM: BM=CN
Cho tam giác ABC có đường trung tuyến BM bằng đường trung tuyến CN. Chứng minh rằng tam giác ABC cân.
Tham khảo:
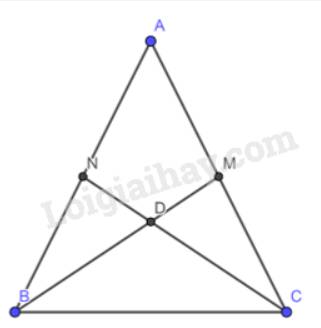
Gọi D là giao điểm của CN và BM
\( \Rightarrow \) D là trọng tâm tam giác ABC
\( \Rightarrow CD = \dfrac{2}{3}CN = BD = \dfrac{2}{3}BM\) ( do BM = CN )
\( \Rightarrow \) tam giác DBC cân tại D do BD = CD
\( \Rightarrow \) \(\widehat {DBC} = \widehat {DCB}\)(2 góc đáy trong tam giác cân) (1)
Xét \(\Delta NDB\) và \(\Delta MDC\) có :
BD = CD
\(\widehat {NDB} = \widehat {MDC}\) (2 góc đối đỉnh)
ND = DM (do cùng \( = \dfrac{1}{3}CN = \dfrac{1}{3}BM\) (tính chất của trung trực đi qua trọng tâm tam giác ))
\( \Rightarrow \Delta NDB=\Delta MDC\) (c.g.c)
\( \Rightarrow \,\widehat {NBD} = \widehat {MCD}\)(2 góc tương ứng) (2)
Từ (1) và (2) \( \Rightarrow \widehat {ABC} = \widehat {ACB}\) do \(\widehat {ABC} = \widehat {NBD} + \widehat {DBC}\) và \(\widehat {ACB} = \widehat {MCD} + \widehat {DCB}\)
\( \Rightarrow \Delta ABC\) cân tại A (do 2 góc bằng nhau)
cho tam giác abc có hai đường trung tuyến bm và cn nếu bm=cn thì tam giác abc là tam giác gì
Do \(BM\) là đường trung tuyến của \(\Delta ABC\) nên ta có: \(AM=CM\)
Và \(CN\) là đường trung tuyến của \(\Delta ABC\) nên ta có: \(AN=BN\)
Mà \(BM=CN\left(gt\right)\)
Từ đó suy ra: \(AM=CM=AN=BN\)
Ta lại có: \(AM+CM=AC\)
Và \(AN+BN=AB\)
Nên: \(AM=CM=AN=BN\)
\(\Rightarrow AM+CM=AN+BN\)
\(\Rightarrow AC=AB\)
Vậy \(\Delta ABC\) có \(AC=AB\) là tam giác cân tại \(A\)
Cho tam giác ABC cân tại A, đường trung tuyến BM. Gọi O là giao điểm các đường trung trực của tam giác ABC. E là trọng tâm của tam giác ABM. CMR : EO vuông góc với BM.
Cho tam giác abc có bd là đường trung tuyến. trong tam giác abd vẽ các trung tuyến am và bm cắt nhau tại h: a, cm dh//bc b,dh=bc/3
Sao vi phạm vậy bạn " Lê Đông Quân "
tnlvprvth học lớp cao
Cho tam giác ABC cân tai A có AH là đường trung tuyến ứng với cạnh BC A)chứng minh tâm giác AHB=tam giác AHC B)kẻ các đường trung tuyến BM và CN .Gọi G là trọng tâm của tam giác ABC Chứng minh tam giác GBC là tam giác cân C)qua C kẻ đường thẳng vuông góc với BC cắt đường thẳng BM tại từ G kẻ đường thẳng song song với BC. Chứng minh BC=2×GD
a: Xet ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
=>ΔAHB=ΔAHC
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
CB chung
=>ΔNBC=ΔMCB
=>góc GBC=góc GCB
=>ΔGCB cân tại G
c: góc ECG+góc BCG=90 độ
góc GBC+góc GEC=90 độ
mà góc BCG=góc GBC
nên góc ECG=góc GEC
=>GC=GE=GB
=>G là trung điểm của BE
Xét ΔEBC có GD//CB
nên GD/CB=EG/EB=1/2
=>CB=2GD
cho tam giác ABC (AB<AC). Trung tuyến BM. Ơ miền ngoài của tam giác ABC , ta dựng các tam giác đều ABE và BCF. Chứng minh EM<FM.