Tính giá trị của biểu thức sau: x= -1,y=2
A: 5+2.(8x+2)
B:2.(y^2 - 4x)
Tính giá trị của biểu thức sau: A=4x-5y/8x-7y. a) Tại x=-2, y=3; b) Biết x/y=5/4
a, Thay x = -2 ; y = 3 ta được
\(A=\dfrac{4\left(-2\right)-5.3}{8\left(-2\right)-7.3}=\dfrac{-8-15}{-16-21}=\dfrac{23}{37}\)
b, Ta có \(\dfrac{x}{y}=\dfrac{5}{4}\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}=k\Rightarrow x=5k;y=4k\)
Thay vào ta được \(A=\dfrac{4.5k-5.4k}{8.5k-7.4k}=\dfrac{0}{40k-28k}=0\)
a)Cho a + b + c = 9, a2 + b2 + c2 = 141. Tính giá trị của biểu thức M =ab + bc + ca
b) Cho x + y = 1 . Tính giá trị của biểu thức B = x3 + 3xy + y3
c) Cho x + y = a ; x2 + b2 = b ; x3 + y3 = c .Tính giá trị của biểu thức N =a3 - 3ab + 2c
d) Cho x + y = a ; x - y = b. Tính giá trị của biểu thức D = x3 - y3 theo a và b
a)Cho a + b + c = 9, a2 + b2 + c2 = 141. Tính giá trị của biểu thức M =ab + bc + ca
b) Cho x + y = 1 . Tính giá trị của biểu thức B = x3 + 3xy + y3
c) Cho x + y = a ; x2 + b2 = b ; x3 + y3 = c .Tính giá trị của biểu thức N =a3 - 3ab + 2c
d) Cho x + y = a ; x - y = b. Tính giá trị của biểu thức D = x3 - y3 theo a và b
a)a+b+c=9
=>(a+b+c)2=81
=>a2+b2+c2+2ab+2bc+2ca=81
Từ a2+b2+c2=141=>2ab+2bc+2ca=81-141=-60
=>2(ab+bc+ca)=-60=>ab+bc+ca=-30
b)x+y=1
=>(x+y)3=1
=>x3+3x2y+3xy2+y3=1
=>x3+y3+3xy(x+y)=1
=>x3+y3+3xy=1(Do x+y=1)
c)a3-3ab+2c=(x+y)3-3(x+y)(x2+y2)+2(x3+y3)
=x3+3x2y+3xy2+y3-3x3-3y3-3x2y-3xy2+2x3+2y3=0
d)đang tìm hướng giải
Rút gọn rồi tính giá trị của biểu thức tại x=1; y=2
A= \(\dfrac{3x}{3x+y}-\dfrac{x}{3x-y}-\dfrac{2x^2}{xy^2-9x^3}\)
ĐK: \(3x\ne\pm y;x\ne0\)
A = \(\dfrac{3x}{3x+y}-\dfrac{x}{3x-y}+\dfrac{2x}{\left(3x-y\right)\left(3x+y\right)}\)
= \(\dfrac{3x\left(3x-y\right)-x\left(3x+y\right)+2x}{\left(3x-y\right)\left(3x+y\right)}=\dfrac{6x^2-4xy+2x}{\left(3x-y\right)\left(3x+y\right)}=\dfrac{2x\left(3x-2y+1\right)}{\left(3x-y\right)\left(3x+y\right)}\)
Thay x = 1; y=2, ta có:
A = \(\dfrac{2.1\left(3.1-2.2+1\right)}{\left(3.1-2\right)\left(3.1+2\right)}=0\)
1.
a)Cho x+y=1.Tính giá trị của biểu thức
1-x3+y3+3xy
b)Cho x-y=1.Tính giá trị biểu thức
x3-y3-3xy
2.Cho x+y=2 và x2+y2=10. Tính giá trị M=x3+y3
b) \(x^3-y^3-3xy\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-3xy\)
\(=\left(x-y\right)\left[\left(x+y\right)^2-2xy+xy\right]-3xy\)
\(=\left(x-y\right)\left(1-xy\right)-3xy\)
\(=x-x^2y-y\)
rút gọn rồi tính giá trị biểu thức tại x=1; y=2
A= \(\dfrac{6x^3-4x^2y+2x^2}{x\left(3x+y\right)\left(3x-y\right)}\)
\(A=\dfrac{2x^2\left(3x-4y+2\right)}{x\left(3x+y\right)\left(3x-y\right)}=\dfrac{2x\left(3x-4y+2\right)}{\left(3x+y\right)\left(3x-y\right)}\\ A=\dfrac{2\left(3-8+2\right)}{\left(3+2\right)\left(3-2\right)}=\dfrac{2\left(-3\right)}{5}=\dfrac{-6}{5}\)
Tính giá trị biểu thức B = y3 + 4x2y + 4xy + 8x3 + 2xy2 với 2xy = 1
Cho biểu thức: B=\(\left[\dfrac{x+1}{2x-2}+\dfrac{3}{x^2-1}-\dfrac{x+3}{2x+2}\right].\dfrac{4x^2-4}{5}\)
a, Tìm điều kiện của x để giá trị của biểu thức được xác định
b, Chứng minh rằng: Khi giá trị của biểu thức được xác định thì nó không phụ thuộc vào giá trị
a, ĐKXĐ: \(x\ne1;x\ne-1\)
b, Với \(x\ne1;x\ne-1\)
\(B=\left[\dfrac{x+1}{2\left(x-1\right)}+\dfrac{3}{\left(x-1\right)\left(x+1\right)}-\dfrac{x+3}{2\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\left[\dfrac{x^2+2x+1+6-x^2-2x+3}{2\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\dfrac{5}{x^2-1}\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =4\)
=> ĐPCM
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
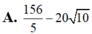
![]()
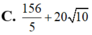
![]()