a)xét tam giác ABD và tam giác EBD,ta có:
góc DEB= góc DAB(=90 độ)
góc EBD=ABD(BD là p/g)
BD chung
Vậy tam giác ABD=tam giác EBD(CẠNH HUYỀN CẠNH GÓC NHỌN)
=>AD=EB
b)xét tam giác ADF và ECD,ta có:
góc CED=FAD(= 90 độ)
DE=DA(cmt)
góc CDE=FDA(đối đỉnh)
=>tam giác ADF=ECD(g.c.g)
=>DF=DC(...)
c)xét tam giácvuông ADF ta có
FD là cạnh huyền
=>AD<FD
có FD=CD(cmt)
=>AD<DC
CHÚC BẠN HỌC TỐT@_@

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có

BE=BA

góc FBE chung

=>ΔBEF=ΔBAC

=>BF=BC

c: ΔBFC cân tại B

mà BD là phân giác

nên BD vuông góc CF

=>BD//AH

=>AH vuông góc AE

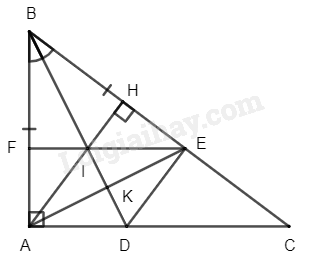
a) Xét \(\Delta ABD\) và \(\Delta EBD\) ta có:

\(BA = BE\) (gt)

\(\widehat {{\rm{ABD}}} = \widehat {{\rm{ EBD}}}\) (do \(BD\) là phân giác)

\(BD\) chung

Suy ra \(\Delta ABD = \Delta EBD\) (c-g-c)

b) Vì \(\Delta ABD = \Delta EBD\) (cmt)

Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{BED}}} = 90^\circ \) (hai góc tương ứng)

Suy ra \(DE \bot BC\)

Mà \(AH \bot BC\) (gt)

Suy ra \(AH\) // \(DE\)

Suy ra \(ADEH\) là hình thang

Mà \(\widehat {{\rm{DEB}}} = 90\) (cmt)

Suy ra \(ADEH\) là hình thang vuông

c) 

Gọi \(K\) là giao điểm của \(AE\) và \(AD\)

Suy ra \(BK\) là phân giác của \(\widehat {{\rm{ABC}}}\)

Mà \(\Delta ABE\) cân tại \(B\) (do \(BA = BE\) )

Suy ra \(BK\) cũng là đường cao

Xét \(\Delta ABE\) có hai đường cao \(BK\) và \(AH\) cắt nhau tại \(I\)

Suy ra \(I\) là trực tâm của \(\Delta ABE\)

Suy ra \(EF \bot AB\)

Mà \(AC \bot AB\) (do \(\Delta ABC\) vuông tại \(A\))

Suy ra \(AC\) // \(EF\)

Suy ra \(ACEF\) là hình thang

Mà \(\widehat {{\rm{CAE}}} = 90^\circ \)(gt)

Suy ra \(ACEF\) là hình thang vuông

thi chua bạn ơi

Chưa thi bn ơi

a, xét 2 t.giác vuông ABD và EBD có:

                 BD cạnh chung

                \(\widehat{ABD}\)=\(\widehat{EBD}\)(gt)

=> t.giác ABD=t.giác EBD(CH-GN)

b,xét 2 t.giác vuông DAF và DEC có:

          DA=DE(theo câu a)

         \(\widehat{ADF}\)=\(\widehat{EDC}\)(vì đối đỉnh)

=> t.giác DAF=t.giác DEC(cạnh góc vuông-góc nhọn kề)

=> DC=DF(2 cạnh tương ứng) mà DF>DA(vì cạnh huyền lớn hơn cạnh góc vuông)

=> DC>DA đpcm

c,xét \(\Delta\)CBK và \(\Delta\)FBK có:

          BK cạnh chung

         \(\widehat{FBK}\)=\(\widehat{CBK}\)(gt)

vì AB=EB mà EC=AF nên suy ra  FB=CB

=> t.giác CBK=t.giác FBK(c.g.c)

=> \(\widehat{FKB}\)=\(\widehat{CKB}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{FKB}\)=\(\widehat{CKB}\)=90 độ

=> BK\(\perp\)CF 

trong t.giác CFB có: FE là đường cao, CA là đường cao

=> BK là đường cao thứ 3 => D là giao điểm của 3 đường cao CA,FE,BK

=> B;D;K thẳng hàng

(câu c mk ko chắc nhé!)

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có

BE=BA

góc EBA chung

=>ΔBEF=ΔBAC

=>BF=BC

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

b: ΔBAD=ΔBED
=>BA=BE và DA=DE

=>BD là trung trực của AE

c: Xét ΔDAK vuông tạiA và ΔDEC vuông tại E có

DA=DE

góc ADK=góc EDC

=>ΔDAK=ΔDEC

=>DK=DC

=>ΔDKC cân tại D

Câu a

Xét tam giác ABD và AMD có

AB = AM từ gt

Góc BAD = MAD vì AD phân giác BAM

AD chung

=> 2 tam guacs bằng nhau

Câu b

Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD

Bd = bm vì 2 tam giác ở câu a bằng nhau

Góc BDE bằng MDC đối đỉnh

=> 2 tam giác bằng nhau

Câu 4: 

a: Xét ΔABD vuông tại B và ΔAED vuông tại E có

AD chung

góc BAD=góc EAD

Do đó: ΔBAD=ΔEAD
b: Ta có: AB=AE

DB=DE

Do đó: AD là đường trung trực của BE

c: Xét ΔBDF vuông tại B và ΔEDC vuông tại E có

DB=DE

góc BDF=góc EDC

Do đó: ΔBDF=ΔEDC

Suy ra: BF=EC