Question

Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\)). Tia phân giác của góc \(B\) cắt \(AC\) tại \(D\). Trên \(BC\) lấy điểm\(E\) sao cho \(BE = BA\).

a) Chứng minh rằng \(\Delta ABD = \Delta EBD\)

b) Kẻ đường cao \(AH\) của tam giác \(ABC\). Chứng minh rằng tứ giác \(ADEH\) là hình thang vuông.

c) Gọi \(I\) là giao điểm của \(AH\) với \(BD\), đường thẳng \(EI\) cắt \(AB\) tại \(F\). Chứng minh rằng tứ giác \(ACEF\) là hình thang vuông.

Answer 1

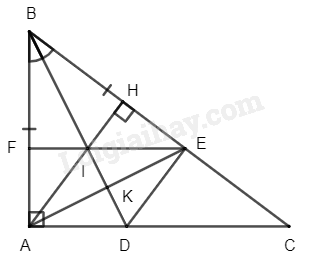
a) Xét \(\Delta ABD\) và \(\Delta EBD\) ta có:

\(BA = BE\) (gt)

\(\widehat {{\rm{ABD}}} = \widehat {{\rm{ EBD}}}\) (do \(BD\) là phân giác)

\(BD\) chung

Suy ra \(\Delta ABD = \Delta EBD\) (c-g-c)

b) Vì \(\Delta ABD = \Delta EBD\) (cmt)

Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{BED}}} = 90^\circ \) (hai góc tương ứng)

Suy ra \(DE \bot BC\)

Mà \(AH \bot BC\) (gt)

Suy ra \(AH\) // \(DE\)

Suy ra \(ADEH\) là hình thang

Mà \(\widehat {{\rm{DEB}}} = 90\) (cmt)

Suy ra \(ADEH\) là hình thang vuông

c) 

Gọi \(K\) là giao điểm của \(AE\) và \(AD\)

Suy ra \(BK\) là phân giác của \(\widehat {{\rm{ABC}}}\)

Mà \(\Delta ABE\) cân tại \(B\) (do \(BA = BE\) )

Suy ra \(BK\) cũng là đường cao

Xét \(\Delta ABE\) có hai đường cao \(BK\) và \(AH\) cắt nhau tại \(I\)

Suy ra \(I\) là trực tâm của \(\Delta ABE\)

Suy ra \(EF \bot AB\)

Mà \(AC \bot AB\) (do \(\Delta ABC\) vuông tại \(A\))

Suy ra \(AC\) // \(EF\)

Suy ra \(ACEF\) là hình thang

Mà \(\widehat {{\rm{CAE}}} = 90^\circ \)(gt)

Suy ra \(ACEF\) là hình thang vuông