Xét ΔOAB có OA=OB(=R)

nên ΔOAB cân tại O(Định nghĩa tam giác cân)

\(\Leftrightarrow\widehat{OAB}=\dfrac{180^0-\widehat{AOB}}{2}\)(Số đo của một góc ở đáy trong ΔOAB cân tại O)

\(\Leftrightarrow\widehat{CAB}=\dfrac{180^0-100^0}{2}=\dfrac{80^0}{2}=40^0\)

Xét (O) có 

ΔCAB nội tiếp đường tròn(C,A,B\(\in\)(O))

AC là đường kính(gt)

Do đó: ΔCAB vuông tại B(Định lí)

\(\Leftrightarrow\widehat{ACB}+\widehat{CAB}=90^0\)(Hai góc nhọn phụ nhau)

\(\Leftrightarrow\widehat{ACB}+40^0=90^0\)

hay \(\widehat{ACB}=50^0\)

Vậy: \(\widehat{ACB}=50^0\)

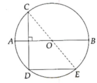
a, Tính được sđ  B E ⏜ = 50 0

b, Chứng minh được sđ  C B E ⏜ = 180 0

=> C, O, E thẳng hàng (ĐPCM)

Tự vẽ hình

a) Do \(CD\) vuông góc \(AB\) nên \(AB\) là trung trực của \(CD\) (liên hệ giữa đường kính và dây cung)

\(\Rightarrow AC=AD\Rightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{AD}\)

Mà \(sđ\stackrel\frown{AC}=\stackrel\frown{AOC}=50^0\Rightarrow sđ\stackrel\frown{AD}=50^0\).

Do \(DE\) song song \(AB\)

\(sđ\stackrel\frown{BE}=sđ\stackrel\frown{AD}=50^0\Rightarrow\widehat{BOE}=sđ\stackrel\frown{BE}=50^0\).

b) Do \(B\in\stackrel\frown{CE}\Rightarrow sđ\stackrel\frown{CBE}=sđ\stackrel\frown{CB}+sđ\stackrel\frown{BE}\)

\(\Rightarrow sđ\stackrel\frown{CBE}=\widehat{COB}+\widehat{BOE}=180^0-\widehat{AOC}+\widehat{BOE}\)

\(\Rightarrow sđ\stackrel\frown{CBE}=180^0-50^0+50^0=180^0\)

\(\Rightarrow\) CE là đường kính

\(\Rightarrow\) C, O, E thẳng hàng.

Xét ΔOAB có OA^2+OB^2=AB^2

và OA=OB

nên ΔOAB vuông cân tại O

Xét ΔACB có

AO là đường trung tuyến, là đường cao

Do đó: ΔACB cân tại A

=>góc ACB+góc ABC=90 độ

=>góc ACB=45 độ

sin ACB=sin45=\(\dfrac{1}{\sqrt{2}}\)

a) Ta có: AB//DE(gt)

CD⊥AB(gt)

Do đó: DE⊥CD(Định lí 2 từ vuông góc tới song song)

⇔\(\widehat{CDE}=90^0\)

Xét ΔCDE có \(\widehat{CDE}=90^0\)(cmt)

nên ΔCDE vuông tại D(Định nghĩa tam giác vuông)

⇔D nằm trên đường tròn đường kính CE

⇔C,D,E nằm trên đường tròn đường kính CE

mà C,D,E cùng nằm trên (O)(gt)

nên CE là đường kính của (O)

hay C,O,E thẳng hàng(đpcm)