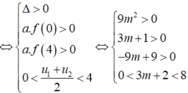cho hàm số (P)y=1/2x^2, tìm m để đường thẳng (d)y=3m-2 luôn cắt (P) tại 2 điểm phân biệt

Những câu hỏi liên quan
a) lập bảng biến thiên và vẽ đồ thị hàm số y = x\(^2\)+3x+2
b) tìm m để đường thẳng y = -x+m cắt (P) tại 2 điểm phân biệt có hoành độ dương
c) tìm m để đường thẳng y = -2x+3m cắt (P) tại 2 điểm phân biệt có hoành độ x1, x2 thỏa mãn x\(_1\)= 3x\(_2\)
Trong mặt phẳng toạ độ Oxy, cho parabol (P): y = x^2 và đường thẳng d: y=2x+|m|+ 1 ( m là tham số ). a) Chứng minh đường thẳng ở luôn cắt (P) tại 2 điểm phân biệt. b) Tìm m để đường thẳng d cắt (P) tại 2 điểm phân biệt có hoành độ x1 x2
a: PTHĐGĐ là:
x^2-2x-|m|-1=0
a*c=-|m|-1<0
=>(d)luôn cắt (P) tại hai điểm phân biệt
b: Bạn bổ sung lại đề đi bạn
Đúng 2
Bình luận (0)
Tìm m để đường thẳng
d
:
y
-
1
cắt đồ thị (C) của hàm số
y
x
4
-
(
3
m
+
2
)
x
2...
Đọc tiếp
Tìm m để đường thẳng d : y = - 1 cắt đồ thị (C) của hàm số y = x 4 - ( 3 m + 2 ) x 2 + 3 m tại bốn điểm phân biệt có hoành độ nhỏ hơn 2
![]()
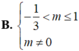
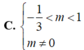
![]()
Cho hàm số
y
x
4
–
(
3
m
+
2
)
x
2
+
3
m
có đồ thị
(
C
m
)
. Tìm m để đường thẳng
d
:
y
-
1
cắt đồ thị
(
C
m
)
tại 4 điểm phân biệt đ...
Đọc tiếp
Cho hàm số y = x 4 – ( 3 m + 2 ) x 2 + 3 m có đồ thị ( C m ) . Tìm m để đường thẳng d : y = - 1 cắt đồ thị ( C m ) tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2
A. - 1 3 < m < 1
B. - 1 2 < m < 1 ; m ≠ 0
C. - 1 2 < m < 1 2 ; m ≠ 0
D. - 1 3 < m < 1 2 ; m ≠ 0
1) cho hàm số y=2x+b. Tìm b để hàm số cắt trục hoành tại điểm có hoành độ bằng 3.
2) Cho Parabol (P): y=x2 và đường thẳng d: y=(m-1)x+m-4. Tìm m để d cắt (P) tại 2 điểm phân biệt nằm về 2 phía của trục tung.
1, Do hàm số trên cắt trục hoành tại điểm có hoành độ bằng 3 hay hàm số trên đi qua A(3;0)
<=> \(0=6+b\Leftrightarrow b=-6\)
2, Hoành độ giao điểm (P) ; (d) tm pt
\(x^2-\left(m-1\right)x-m+4=0\)
Để (P) cắt (d) tại 2 điểm pb nằm về 2 phía trục tung khi pt có 2 nghiệm trái dấu hay
\(x_1x_2=-m+4< 0\Leftrightarrow-m< -4\Leftrightarrow m>4\)
a) vẽ đồ thị hàm số y=2x^2 (P). b) chứng mình đường thẳng (d): y=2mx-m+1 luôn cắt (P) tại 2 điểm phân biệt
a) bạn tự vẽ nha
b) pt hoành độ giao điểm: \(2x^2-2mx+m-1=0\)
\(\Delta=4m^2-8\left(m-1\right)=4\left(m-1\right)^2+4>0\)
\(\Rightarrow\) pt luôn có 2 nghiệm phân biệt
Đúng 0
Bình luận (0)
Cho hàm số y=x2 có đồ thị là (P). Tìm m để đường thẳng (d): y=2x-3m cắt (P) tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn: x1.x22 -x2(3m+2x1)=12
Phương trình hoành độ giao điểm: \(x^2=2x-3m\Leftrightarrow x^2-2x+3m=0\) (1)
(P) cắt (d) tại 2 điểm khi (1) có 2 nghiệm \(\Rightarrow\Delta'=1-3m\ge0\Rightarrow m\le\dfrac{1}{3}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=3m\end{matrix}\right.\)
\(x_1.x_2^2-x_2\left(3m+2x_1\right)=12\)
\(\Leftrightarrow x_1x_2.x_2-3mx_2-2x_1x_2=12\)
\(\Leftrightarrow3mx_2-3mx_2-6m=12\)
\(\Rightarrow m=-2\)
Đúng 0
Bình luận (0)
Bài 1: Tìm m để đường thẳng y= 2x-1-3m và y= 3x+m cắt nhau tại 1 điểm trên trục hoành.
Bài 2: Cho hàm số y= mx+m-2. Tìm m biết rằng đồ thị hàm số đã cho cắt đường thẳng y= 2x+1 tại một điểm có tung độ bằng 3.
cho hàm số y=1/2x^2 có đồ thị (P). Tìm m để đg thẳng d: y=3mx-2 cắt (P) tại 2 điểm phân biệt
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2-3mx+2=0\)
\(\text{Δ}=\left(-3m\right)^2-4\cdot\dfrac{1}{2}\cdot2=9m^2-4\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow\left[{}\begin{matrix}m>\dfrac{2}{3}\\m< -\dfrac{2}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)