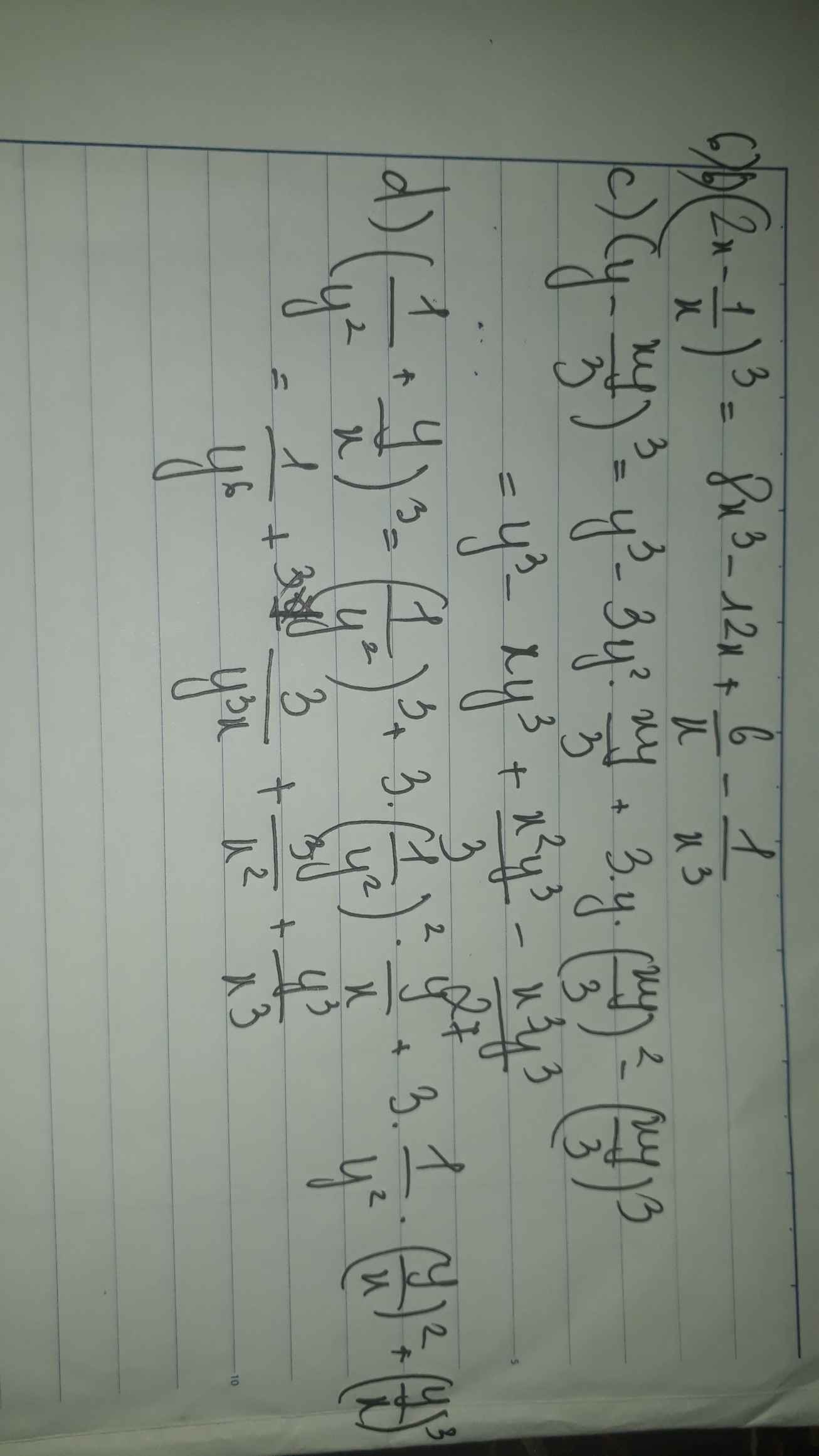Câu 1:

Ta có 2x - y = 8 => 2x - y + 9 = 17

Mà 3x + y = 17 => 2x - y + 9 = 3x + y

<=> 9 - y = x + y <=> 9 = x + 2y <=> x = 9 - 2y

Mà 2x - y = 8 => 18 - 4y - y = 8 => 18 - 5y = 8 => y = 2 => x = 5

Bài `13`

\(a,\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\\ =\sqrt{9\cdot3}+\sqrt{16\cdot3}-\sqrt{36\cdot3}-\sqrt{4\cdot3}\\ =3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}\\ =\left(3+4-6-2\right)\sqrt{3}\\ =-\sqrt{3}\\ b,\left(\sqrt{28}+\sqrt{12}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\\ =\left(\sqrt{4\cdot7}+\sqrt{4\cdot3}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{4\cdot21}\\ =\left(2\sqrt{7}+2\sqrt{3}-\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\\ =2\cdot7+2\sqrt{21}-7+2\sqrt{21}\\ =14+2\sqrt{21}-7+2\sqrt{21}\\ =7+4\sqrt{21}\)

17:
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >4\end{matrix}\right.\)

Để A là số nguyên thì \(\sqrt{x}-1⋮\sqrt{x}-2\)

=>\(\sqrt{x}-2+1⋮\sqrt{x}-2\)

=>\(\sqrt{x}-2\in\left\{1;-1\right\}\)

=>\(\sqrt{x}\in\left\{3;1\right\}\)

=>\(x\in\left\{9;1\right\}\)

16:

a: BC=BH+CH

=9+16

=25(cm)

Xét ΔABC vuông tại A có AH là đường cao

nên \(AH^2=HB\cdot HC\)

=>\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{9\cdot25}=15\left(cm\right)\\AC=\sqrt{16\cdot25}=20\left(cm\right)\end{matrix}\right.\)

b: M là trung điểm của AC

=>AM=AC/2=10(cm)

Xét ΔAMB vuông tại A có

\(tanAMB=\dfrac{AB}{AM}=\dfrac{15}{10}=\dfrac{3}{2}\)

nên \(\widehat{AMB}\simeq56^0\)

tu ma lam hoc nhu ngu cung hoc de rua

Đặt tích 3 số tự nhiên liên tiếp là  a * (a + 1) * (a + 2)

 +Nếu a = 2k  thì:

a * (a + 1) * (a + 2) chia hết cho 2

+ Nếu a = 2k +1 thì:

a+1=2k+1+1=2k+2 chia hết cho 2

Suy ra a * (a + 1) * (a + 2) chia hết cho 2

+ Nếu a = 3k thì

a * (a + 1) * (a + 2) chia hết cho 3

+ Nếu a = 3k +1 thì

a+2=3k+1+2=3k+3 chia hết cho 3

Suy ra a * (a + 1) * (a + 2) chia hết cho 3

+ Nếu a = 3k+2 thì:

a+1=3k+2+1=3k+3 chia hết cho 3

Suy ra a * (a + 1) * (a + 2) chia hết cho 3

Vì 2 và 3 nguyên tố cùng nhau nên a * (a + 1) * (a + 2) chia hết cho 2.3=6 (đpcm)

123 vì 1:6=6      2:6=3             3:6=2

2/5 thế kỉ = 200 / 5 = 40 năm

Câu 4:

Đ

S

Đ

S

Câu 7b, \(3+\dfrac{4}{7}=\dfrac{3}{1}+\dfrac{4}{7}=\dfrac{21}{7}+\dfrac{4}{7}=\dfrac{25}{7}\)(bn đặt tính sai r)

Sửa tới đó thôi lười qá :v, từ câu 1 đến câu 7 bn sai chừng đó đó :v, còn lại đúg r :v

4.

\(ab+bc+ca=3abc\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\)

Đặt \(\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)

\(S=\sum\dfrac{\dfrac{1}{y^2}}{\dfrac{1}{x}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)}=\sum\dfrac{x^3}{x^2+y^2}=\sum\left(x-\dfrac{xy^2}{x^2+y^2}\right)\)

\(S\ge\sum\left(x-\dfrac{xy^2}{2xy}\right)=\sum\left(x-\dfrac{y}{2}\right)=\dfrac{x+y+z}{2}=\dfrac{3}{2}\)

\(S_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)

5.

Đặt \(\left(\dfrac{1}{a};\dfrac{2}{b};\dfrac{3}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)

Đặt vế trái là P

\(P=\dfrac{z^3}{x^2+z^2}+\dfrac{x^3}{x^2+y^2}+\dfrac{y^3}{y^2+z^2}\)

Quay lại dòng 3 của bài số 4

6.

Do a;b;c không âm, ta có:

\(b^2\left(b-1\right)^2\left(b+2\right)\ge0\)

\(\Leftrightarrow b^5-3b^3+2b^2\ge0\)

\(\Leftrightarrow b^5-3b^3+2b^2-6\ge-6\)

\(\Leftrightarrow-\left(3-b^2\right)\left(b^3+2\right)\ge-6\)

\(\Leftrightarrow6\ge\left(3-b^2\right)\left(b^3+2\right)\)

\(\Rightarrow\dfrac{1}{b^3+2}\ge\dfrac{3-b^2}{6}\)

\(\Rightarrow\dfrac{a}{b^3+2}\ge\dfrac{a\left(3-b^2\right)}{6}\)

Tương tự: \(\dfrac{b}{c^3+2}\ge\dfrac{b\left(3-c^2\right)}{6}\) ; \(\dfrac{c}{a^3+2}\ge\dfrac{c\left(3-a^2\right)}{6}\)

Cộng vế: \(P\ge\dfrac{a+b+c}{2}-\dfrac{ab^2+bc^2+ca^2+abc}{6}=\dfrac{3}{2}-\dfrac{ab^2+bc^2+ca^2+abc}{6}\)

Không mất tính tổng quát, giả sử \(b=mid\left\{a;b;c\right\}\)

\(\left(b-a\right)\left(b-c\right)\le0\)

\(\Leftrightarrow b^2+ac\le ab+bc\)

\(\Leftrightarrow ab^2+ca^2\le a^2b+abc\)

\(\Rightarrow ab^2+bc^2+ca^2+abc\le bc^2+a^2b+2abc=b\left(a+c\right)^2=4b\left(\dfrac{a+c}{2}\right)\left(\dfrac{a+c}{2}\right)\le\dfrac{4}{27}\left(a+b+c\right)^3=4\)

\(\Rightarrow P\ge\dfrac{3}{2}-\dfrac{4}{6}=\dfrac{5}{6}\)

Positive feelings: calm; delighted; relaxed; confident
Negative feelings: worried; depressed; left out; embarrassed; frustrated

Giúp em với ạ 

Positive

worried, depressed, left out, embarrassed, frustrated

Negative

calm, delighted, relaxed, confident

Chúc bạn thi tốt nha!

a) Ta có: \(\left(3x+1\right)^3\)

\(=\left(3x\right)^3+3\cdot\left(3x\right)^2\cdot1+3\cdot3x\cdot1^2+1^3\)

\(=27x^3+27x^2+9x+1\)

b) Ta có: \(\left(2x-\dfrac{1}{x}\right)^3\)

\(=\left(2x\right)^3-3\cdot\left(2x\right)^2\cdot\dfrac{1}{x}+3\cdot2x\cdot\left(\dfrac{1}{x}\right)^2-\left(\dfrac{1}{x}\right)^3\)

\(=8x^3-12x+\dfrac{6}{x}-\dfrac{1}{x^3}\)

Số tuổi anh hơn em là: 14-5 = 9 tuổi.
Hiệu số phần là " 2-1 = 1 phần
Số tuổi của anh khi gấp em 2 lần là: 9: 1 x 2 = 18 tuổi
Vậy sau số năm tuổi anh gấp 2 lần tuổi em là: 18-14 = 4 năm

Hiệu số tuổi của 2 anh em là:

14 - 5 = 9 ( tuổi )

Gấp 2 => tỉ số là \(\frac{1}{2}\)

Hiệu số phần bằng nhau là:

2 - 1 = 1 ( phần )

Tuổi của em khi gấp lên 2 là:

9: 1 x 1 = 9 ( tuổi )

=> sau số năm nữa tuổi anh gấp 2 lần tuổi em:

9 - 5 = 4 ( năm )

Vậy sau 4 năm nữa thì tuổi anh sẽ gấp 2 lần tuổi em.

Bài 6:

a. \(A=[\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{2}{\sqrt{x}(\sqrt{x}-1)}].(\sqrt{x}-1)\)

\(=\sqrt{x}+\frac{2}{\sqrt{x}}=\frac{x+2}{\sqrt{x}}\)

b. Áp dụng BĐT Cô-si cho các số dương:

$A=\sqrt{x}+\frac{2}{\sqrt{x}}\geq 2\sqrt{2}$

Vậy gtnn của $A$ là $2\sqrt{2}$. Giá trị này đạt tại $x=2$

Bài 7:

a.

\(x=\frac{1}{\sqrt{3}-1}-\frac{1}{\sqrt{3}+1}=1\)

Khi đó: \(B=\frac{1+3}{1+8}=\frac{4}{9}\)

b. \(A=\frac{(\sqrt{x}+1)(\sqrt{x}+3)+\sqrt{x}(2\sqrt{x}-1)}{(2\sqrt{x}-1)(\sqrt{x}+3)}-\frac{x+6\sqrt{x}+2}{(2\sqrt{x}-1)(\sqrt{x}+3)}\)

\(=\frac{3x+3\sqrt{x}+3-(x+6\sqrt{x}+2)}{(\sqrt{x}+3)(2\sqrt{x}-1)}=\frac{2x-3\sqrt{x}+1}{(2\sqrt{x}-1)(\sqrt{x}+3)}\)

\(=\frac{(2\sqrt{x}-1)(\sqrt{x}-1)}{(2\sqrt{x}-1)(\sqrt{x}+3)}=\frac{\sqrt{x}-1}{\sqrt{x}+3}\)

c.

\(P=AB=\frac{\sqrt{x}+3}{x+8}.\frac{\sqrt{x}-1}{\sqrt{x}+3}=\frac{\sqrt{x}-1}{x+8}\)

Áp dụng BĐT Cô-si:

$x+16\geq 8\sqrt{x}$

$\Rightarrow x+8\geq 8(\sqrt{x}-1)$

$\Rightarrow P\leq \frac{\sqrt{x}-1}{8(\sqrt{x}-1)}=\frac{1}{8}$

Vậy $P_{\max}=\frac{1}{8}$ khi $x=16$

Bài 8:

a. \(A=\frac{9+\sqrt{9}+4}{\sqrt{9}-2}=16\)

b. \(B=\frac{3x-4}{\sqrt{x}(\sqrt{x}-2)}-\frac{(\sqrt{x}+2)(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}-\frac{\sqrt{x}(\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-2)}\)

\(=\frac{3x-4-(x-4)-(x-\sqrt{x})}{\sqrt{x}(\sqrt{x}-2)}=\frac{x+\sqrt{x}}{\sqrt{x}(\sqrt{x}-2)}=\frac{\sqrt{x}+1}{\sqrt{x}-2}\) (đpcm)

c. Áp dụng BĐT Cô-si:

\(P=A:B=\frac{x+\sqrt{x}+4}{\sqrt{x}-2}:\frac{\sqrt{x}+1}{\sqrt{x}-2}=\frac{x+\sqrt{x}+4}{\sqrt{x}+1}\)

\(=\sqrt{x}+\frac{4}{\sqrt{x}+1}=(\sqrt{x}+1)+\frac{4}{\sqrt{x}+1}-1\geq 2\sqrt{4}-1=3\)

Vậy $P_{\min}=3$ khi $x=1$

Bài 3:

theo đề bài ta có:

\(\left\{{}\begin{matrix}2a-3b=0\\5b-7c=0\\3a-7b+5c=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=42\\b=28\\c=20\end{matrix}\right.\)

Bài 4: 

Đặt \(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}=k\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=4k\\y=5k\\z=6k\end{matrix}\right.\)

Ta có: \(x^2-2y^2+z^2=18\)

\(\Leftrightarrow16k^2-50k^2+36k^2=18\)

\(\Leftrightarrow k^2=9\)

Trường hợp 1: k=3

\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=4\cdot3=12\\y=5k=5\cdot3=15\\z=6k=6\cdot3=18\end{matrix}\right.\)

Trường hợp 2: k=-3

\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=-3\cdot4=-12\\y=5k=-3\cdot5=-15\\z=6k=-3\cdot6=-18\end{matrix}\right.\)