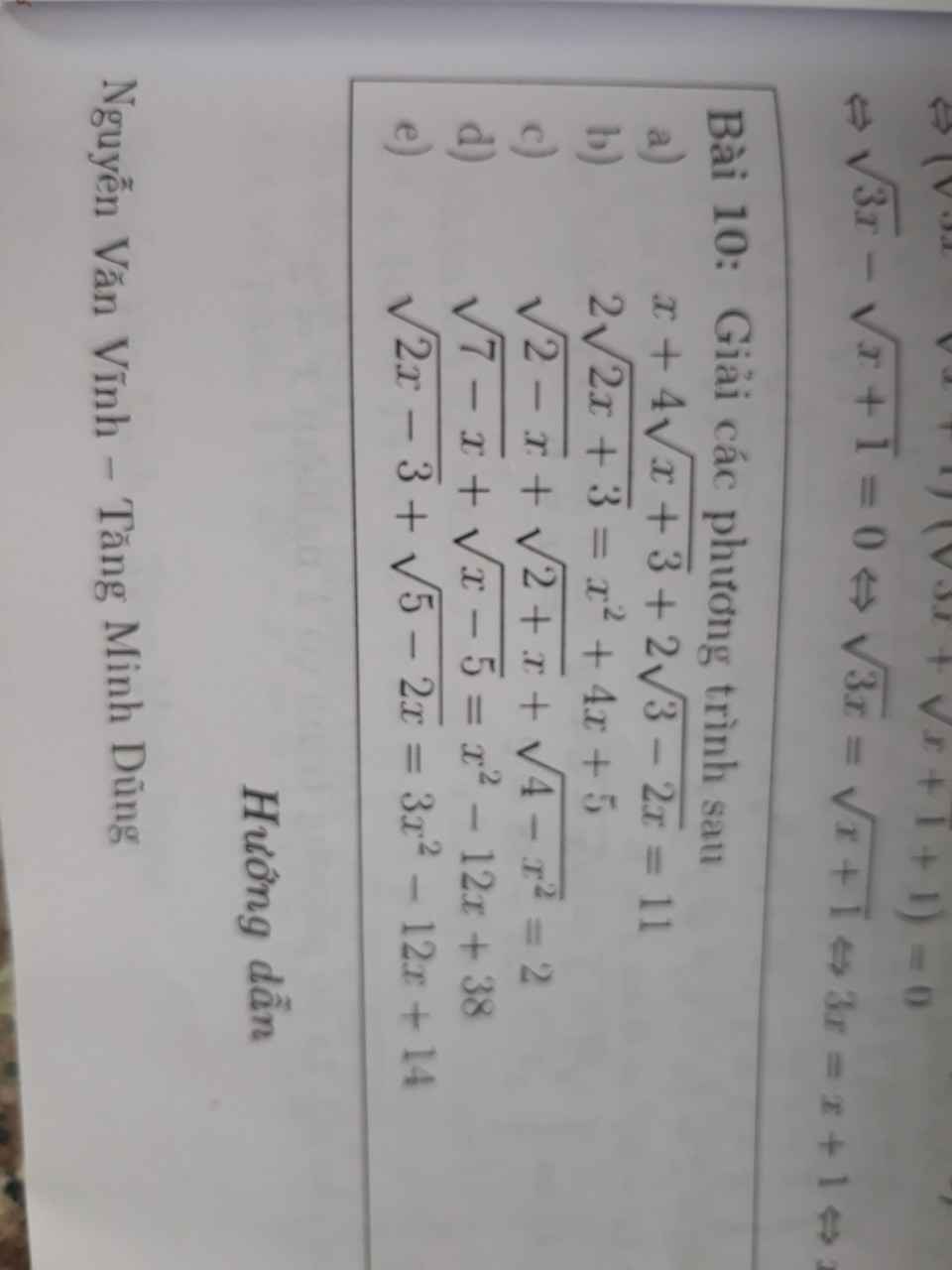Bài 6:
a. \(A=[\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{2}{\sqrt{x}(\sqrt{x}-1)}].(\sqrt{x}-1)\)
\(=\sqrt{x}+\frac{2}{\sqrt{x}}=\frac{x+2}{\sqrt{x}}\)
b. Áp dụng BĐT Cô-si cho các số dương:
$A=\sqrt{x}+\frac{2}{\sqrt{x}}\geq 2\sqrt{2}$
Vậy gtnn của $A$ là $2\sqrt{2}$. Giá trị này đạt tại $x=2$
Bài 7:
a.
\(x=\frac{1}{\sqrt{3}-1}-\frac{1}{\sqrt{3}+1}=1\)
Khi đó: \(B=\frac{1+3}{1+8}=\frac{4}{9}\)
b. \(A=\frac{(\sqrt{x}+1)(\sqrt{x}+3)+\sqrt{x}(2\sqrt{x}-1)}{(2\sqrt{x}-1)(\sqrt{x}+3)}-\frac{x+6\sqrt{x}+2}{(2\sqrt{x}-1)(\sqrt{x}+3)}\)
\(=\frac{3x+3\sqrt{x}+3-(x+6\sqrt{x}+2)}{(\sqrt{x}+3)(2\sqrt{x}-1)}=\frac{2x-3\sqrt{x}+1}{(2\sqrt{x}-1)(\sqrt{x}+3)}\)
\(=\frac{(2\sqrt{x}-1)(\sqrt{x}-1)}{(2\sqrt{x}-1)(\sqrt{x}+3)}=\frac{\sqrt{x}-1}{\sqrt{x}+3}\)
c.
\(P=AB=\frac{\sqrt{x}+3}{x+8}.\frac{\sqrt{x}-1}{\sqrt{x}+3}=\frac{\sqrt{x}-1}{x+8}\)
Áp dụng BĐT Cô-si:
$x+16\geq 8\sqrt{x}$
$\Rightarrow x+8\geq 8(\sqrt{x}-1)$
$\Rightarrow P\leq \frac{\sqrt{x}-1}{8(\sqrt{x}-1)}=\frac{1}{8}$
Vậy $P_{\max}=\frac{1}{8}$ khi $x=16$
Bài 8:
a. \(A=\frac{9+\sqrt{9}+4}{\sqrt{9}-2}=16\)
b. \(B=\frac{3x-4}{\sqrt{x}(\sqrt{x}-2)}-\frac{(\sqrt{x}+2)(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}-\frac{\sqrt{x}(\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-2)}\)
\(=\frac{3x-4-(x-4)-(x-\sqrt{x})}{\sqrt{x}(\sqrt{x}-2)}=\frac{x+\sqrt{x}}{\sqrt{x}(\sqrt{x}-2)}=\frac{\sqrt{x}+1}{\sqrt{x}-2}\) (đpcm)
c. Áp dụng BĐT Cô-si:
\(P=A:B=\frac{x+\sqrt{x}+4}{\sqrt{x}-2}:\frac{\sqrt{x}+1}{\sqrt{x}-2}=\frac{x+\sqrt{x}+4}{\sqrt{x}+1}\)
\(=\sqrt{x}+\frac{4}{\sqrt{x}+1}=(\sqrt{x}+1)+\frac{4}{\sqrt{x}+1}-1\geq 2\sqrt{4}-1=3\)
Vậy $P_{\min}=3$ khi $x=1$
Bài 9:
a.
\(B=\frac{x\sqrt{x}+3x-3x-1}{\sqrt{x}(\sqrt{x}+3)}.\frac{\sqrt{x}+3}{\sqrt{x}-1}=\frac{x\sqrt{x}-1}{\sqrt{x}(\sqrt{x}-1)}=\frac{(\sqrt{x}-1)(x+\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}-1)}=\frac{x+\sqrt{x}+1}{\sqrt{x}}\)
b.
\(P=AB=\frac{\sqrt{x}}{\sqrt{x}-1}.\frac{x+\sqrt{x}+1}{\sqrt{x}}=\frac{x+\sqrt{x}+1}{\sqrt{x}-1}\)
Với điều kiện trên thì không có min P.
Bài 10:
a. $x=4-2\sqrt{3}=(\sqrt{3}-1)^2$
$\Rightarrow \sqrt{x}=\sqrt{3}-1$
\(Q=\frac{\sqrt{3}-1-1}{\sqrt{3}-1-3}=\frac{5-2\sqrt{3}}{13}\)
b.
\(P=\frac{2\sqrt{x}(\sqrt{x}-3)+\sqrt{x}(\sqrt{x}+3)}{(\sqrt{x}+3)(\sqrt{x}-3)}-\frac{3x+3}{(\sqrt{x}-3)(\sqrt{x}+3)}\)
\(=\frac{-3(\sqrt{x}+1)}{(\sqrt{x}-3)(\sqrt{x}+3)}\)
\(M=P:Q=\frac{-3(\sqrt{x}+1)}{(\sqrt{x}-3)(\sqrt{x}+3)}:\frac{\sqrt{x}+1}{\sqrt{x}-3}=\frac{-3}{\sqrt{x}+3}\)
c.
\(A=xM+\frac{4x+7}{\sqrt{x}+3}=\frac{-3x}{\sqrt{x}+3}+\frac{4x+7}{\sqrt{x}+3}=\frac{x+7}{\sqrt{x}+3}\)
Áp dụng BĐT Cô-si:
$x+1\geq 2\sqrt{x}\Rightarrow x+7\geq 2(\sqrt{x}+3)$
$\Rightarrow A\geq 2$
Vậy gtnn của $A$ là $2$ khi $x=1$