Mẫu số liệu thống kê ở Hoạt động 1 đã được ghép thành năm nhóm ứng với năm nửa khoảng: [150; 155), [155; 160), [160; 165), [165; 170), [170; 175).
Có bao nhiêu số liệu trong mẫu số liệu đó thuộc vào nhóm 1?
Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong một tuần (đơn vị: kilomet) của 40 chiếc ô tô:

a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy với năm nhóm ứng với năm nửa khoảng: [100 ; 120), [120 ; 140), [140 ; 160), [160 ; 180), [180 ; 200)
b) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
c) Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu?
a, Bảng tần số ghép nhóm cho mẫu số liệu trên có tám nhóm ứng với tám nửa khoảng:
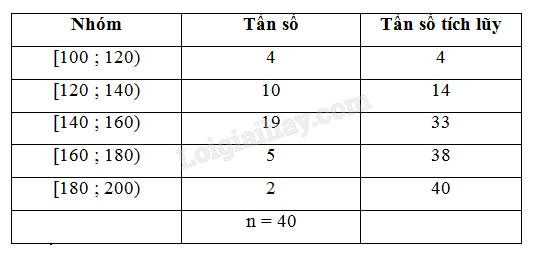
b, - Trung bình cộng là:
\(\overline{x}=\dfrac{110\cdot4+130\cdot15+150\cdot14+170\cdot5+190\cdot2}{40}=143\)
- Trung vị là: \(M_e=140+\left(\dfrac{20-19}{14}\right)\cdot20\simeq141\)
- \(Q_1=120+\left(\dfrac{10-4}{15}\right)\cdot20\simeq128\\ Q_2=M_e\simeq141\\ Q_3=140+\left(\dfrac{30-19}{15}\right)\cdot20=155,6\)
c, Mốt của mẫu số liệu là:
Có nhóm 2 là nhóm có tần số lớn nhất
\(\Rightarrow M_o=120+\left(\dfrac{15-4}{2\cdot15-4-14}\right)\cdot20\simeq138,3\)
Một cửa hàng đã thống kê số ba lỗ bán được mỗi ngày trong tháng 9 với kết quả cho như sau:

Hãy chia mẫu số liệu trên thành 5 nhóm, lập tần số ghép nhóm, hiệu chỉnh bảng và xác định giá trị đại diện cho mỗi nhóm.
Tham khảo:
Khoảng biến thiên của mẫu số liệu trên là \(R = 29 - 10 = 19\).
Độ dài mỗi nhóm \(L > \frac{R}{k} = \frac{{19}}{5} = 3,8\).
Ta chọn \(L = 4\) và chia dữ liệu thành các nhóm: \(\left[ {10;14} \right),\left[ {14;18} \right),\left[ {18;22} \right),\left[ {22;26} \right),\left[ {26;30} \right)\).
Khi đó ta có bảng tần số ghép nhóm sau:

Một phòng khám thống kê số bệnh nhân đến khám bệnh mỗi ngày trong tháng 4 năm 2022 ở bảng sau:

a) Hãy ước lượng các tử phân vị của mẫu số liệu ghép nhóm trên.
b) Quản lí phòng khám cho rằng có khoảng 25% số ngày khám có nhiều hơn 35 bệnh nhân đến khám. Nhận định trên có hợp lí không?
a) Do số bệnh nhân là số nguyên nên ta hiệu chỉnh như sau:

Số bệnh nhân đến khám bệnh mỗi ngày trong tháng 4 năm 2022 là:
\(n = 7 + 8 + 7 + 6 + 2 = 30\).
Gọi \({x_1};{x_2};...;{x_{30}}\) là số bệnh nhân đến khám bệnh mỗi ngày được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_7} \in \begin{array}{*{20}{l}}{\left[ {0,5;10,5} \right)}\end{array};{x_8},...,{x_{15}} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array};{x_{16}},...,{x_{22}} \in \begin{array}{*{20}{l}}{\left[ {20,5;30,5} \right)}\end{array};\\{x_{23}},...,{x_{28}} \in \begin{array}{*{20}{l}}{\left[ {30,5;40,5} \right)}\end{array};{x_{29}},{x_{30}} \in \begin{array}{*{20}{l}}{\left[ {40,5;50,5} \right)}\end{array}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\)
Do \({x_{15}} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array},{x_{16}} \in \begin{array}{*{20}{l}}{\left[ {20,5;30,5} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = 20,5\).
• Tứ phân vị thứ nhất của dãy số liệu là: \({x_8}\).
Ta có: \(n = 30;{n_m} = 8;C = 7;{u_m} = 10,5;{u_{m + 1}} = 20,5\)
Do \({x_8} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{30}}{4} - 7}}{8}.\left( {20,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \({x_{23}}\).
Ta có: \(n = 30;{n_j} = 6;C = 7 + 8 + 7 = 22;{u_j} = 30,5;{u_{j + 1}} = 40,5\)
Do \({x_{23}} \in \begin{array}{*{20}{l}}{\left[ {30,5;40,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 30,5 + \frac{{\frac{{3.30}}{4} - 22}}{6}.\left( {40,5 - 30,5} \right) \approx 31,3\)
b) Do \({Q_3} \approx 31,3\) nên nhận định trên hợp lí.
Biểu đồ đoạn thẳng ở Hình 4 biểu diễn giá vàng bán ra trong bảy ngày đầu tiên của tháng 6 năm 2021.
a) Viết mẫu số liệu thống kê giá vàng bán ra nhận được từ biểu đồ ở Hình 4.
b) Tìm khoảng biến thiên của mẫu số liệu đó.
c) Tìm khoảng tứ phân vị của mẫu số liệu đó.
d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
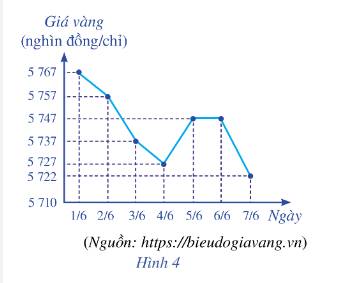
a) Dựa vào biểu đồ, ta có mẫu số liệu là:
5767 5757 5737 5727 5747 5747 5722
b) Khoảng biến thiên của mẫu số liệu đó là: \(R = {x_{\max }} - {x_{\min }} = 5767 - 5722 = 45\)
c) +) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5722 5727 5737 5747 5747 5757 5767
+) Các tứ phân vị của mẫu số liệu là:
Trung vị của mẫu số liệu: \({Q_2}\) = 5747.
Trung vị của dãy 5722 5727 5737 là: \({Q_1}\) = 5727.
Trung vị của dãy 5747 5757 5767 là: \({Q_3}\) = 5757.
+) Khoảng tứ phân vị của mẫu số liệu là: \({\Delta _Q} ={Q_3} - {Q_1}\) = 5757- 5727= 30.
d) +) Giá vàng trung bình trong 7 ngày đầu tiên của tháng 6 năm 2021 là: \(\overline x = \frac{{5722{\rm{ + }}5727{\rm{ + }}5737{\rm{ + }}5747{\rm{ + }}5747{\rm{ + }}5757{\rm{ + }}5767}}{7} = 5743,43\) ( nghìn đồng/ chỉ)
+) Phương sai của mẫu số liệu là: \({s^2} = \frac{{\left[ {{{\left( {5722 - \overline x } \right)}^2} + {{\left( {5727 - \overline x } \right)}^2} + ... + {{\left( {5767 - \overline x } \right)}^2}} \right]}}{7} \approx 219,39\)
+) Độ lệch chuẩn của của mẫu số liệu là: \(s = \sqrt {{s^2}} = \sqrt {219,39} \approx 14,81\)( nghìn đồng/ chỉ)
Đề bài
Một thư viện thống kê số lượng sách được mượn mỗi ngày trong ba tháng ở bảng sau:

Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.
Tham khảo:
Do số quyển sách là số nguyên nên ta hiệu chỉnh lại như sau:

Số sách trung bình được mượn mỗi ngày sau khi ghép nhóm là:
\(\bar x = \frac{{3.18 + 6.23 + 15.28 + 27.33 + 22.38 + 14.43 + 5.48}}{{92}} \approx 34,6\)
Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {30,5;35,5} \right)\).
Do đó: \({u_m} = 30,5;{n_{m - 1}} = 15;{n_m} = 27;{n_{m + 1}} = 22;{u_{m + 1}} - {u_m} = 35,5 - 30,5 = 5\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 30,5 + \frac{{27 - 15}}{{\left( {27 - 15} \right) + \left( {27 - 22} \right)}}.5 \approx 34\)
Vậy số lượng sách được mượn mỗi ngày cao nhất là 35 quyển.
Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau:
Hãy ước lượng số trung bình, tứ phân vị và mốt của mẫu số liệu ghép nhóm trên.
Tổng số học sinh: \(n = 8 + 10 + 16 + 24 + 13 + 7 + 4 = 82\)
• Điểm trung bình môn Toán của các học sinh lớp 11 trên là:
\(\bar x = \frac{{8.6,75 + 10.7,25 + 16.7,75 + 24.8,25 + 13.8,75 + 7.9,25 + 4.9,75}}{{82}} = 8,12\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {8;8,5} \right)\).
Do đó: \({u_m} = 8;{n_{m - 1}} = 16;{n_m} = 24;{n_{m + 1}} = 13;{u_{m + 1}} - {u_m} = 8,5 - 8 = 0,5\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{24 - 16}}{{\left( {24 - 16} \right) + \left( {24 - 13} \right)}}.0,5 \approx 8,21\)
• Gọi \({x_1};{x_2};...;{x_{82}}\) là điểm của các học sinh lớp 11 được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_8} \in \begin{array}{*{20}{c}}{\left[ {6,5;7} \right)}\end{array};{x_9},...,{x_{18}} \in \begin{array}{*{20}{c}}{\left[ {7;7,5} \right)}\end{array};{x_{19}},...,{x_{34}} \in \begin{array}{*{20}{c}}{\left[ {7,5;8} \right)}\end{array};{x_{35}},...,{x_{58}} \in \begin{array}{*{20}{c}}{\left[ {8;8,5} \right)}\end{array};\\{x_{59}},...,{x_{71}} \in \begin{array}{*{20}{c}}{\left[ {8,5;9} \right)}\end{array};{x_{72}},...,{x_{78}} \in \begin{array}{*{20}{c}}{\left[ {9;9,5} \right)}\end{array};{x_{79}},...,{x_{82}} \in \begin{array}{*{20}{c}}{\left[ {9,5;10} \right)}\end{array}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{41}} + {x_{42}}} \right)\)
Ta có: \(n = 82;{n_m} = 24;C = 8 + 10 + 16 = 34;{u_m} = 8;{u_{m + 1}} = 8,5\)
Do \({x_{41}},{x_{42}} \in \begin{array}{*{20}{l}}{\left[ {8;8,5} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{\frac{{82}}{2} - 34}}{{24}}.\left( {8,5 - 8} \right) \approx 8,15\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_{21}}\).
Ta có: \(n = 82;{n_m} = 16;C = 8 + 10 = 18;{u_m} = 7,5;{u_{m + 1}} = 8\)
Do \({x_{21}} \in \begin{array}{*{20}{l}}{\left[ {7,5;8} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 7,5 + \frac{{\frac{{82}}{4} - 18}}{{16}}.\left( {8 - 7,5} \right) \approx 7,58\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{62}}\).
Ta có: \(n = 82;{n_j} = 13;C = 8 + 10 + 16 + 24 = 58;{u_j} = 8,5;{u_{j + 1}} = 9\)
Do \({x_{62}} \in \begin{array}{*{20}{l}}{\left[ {8,5;9} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 8,5 + \frac{{\frac{{3.82}}{4} - 58}}{{13}}.\left( {9 - 8,5} \right) \approx 8,63\)
Cho bảng số liệu:
LAO ĐỘNG TỪ 15 TUỔI TRỞ LÊN PHÂN THEO NHÓM TUỔI Ở VIỆT NAM
GIAI ĐOẠN 2010 – 2015
(Đơn vị: nghìn người)
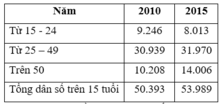
(Nguồn: Niên giám thống kê Việt Nam năm 2015, NXB Thống kê, 2016)
Nhận xét nào sau đây đúng với sự thay đổi lao động từ 15 tuổi trở lên phân theo nhóm tuổi ở Việt Nam giai đoạn 2010 – 2015?
A. Lao động trên 50 tuổi ít nhất.
B. Lao động từ 15 – 24 tuổi tăng.
C. Lao động trên 50 tuổi giảm.
D. Lao động từ 24 – 49 tuổi tăng.
Cho bảng số liệu:
KẾT QUẢ HOẠT ĐỘNG BƯU CHÍNH VIỄN THÔNG Ở NƯỚC TA,
GIAI ĐOẠN 2010 – 2015
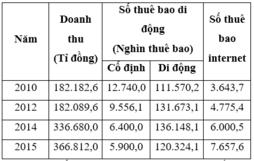
(Nguồn: Niên giám thống kê Việt Nam năm 2015, Nhà xuất bản Thống kê, 2016)
Căn cứ vào bảng trên, hãy cho biết nhận xét nào sau đay đúng với kết quả hoạt động bưu chính viễn thông ở nước ta, giai đoạn 2010 – 2015?
A. Doanh thu giảm chậm.
B. Số thuê bao cố định tăng chậm.
C. Số thuê bao di động giảm chậm.
D. Số thuê bao internet tăng nhanh.
Cho bảng số liệu:
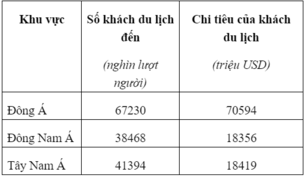
SỐ KHÁCH DU LỊCH QUỐC TẾ ĐẾN VÀ CHI TIÊU CỦA KHÁCH DU LỊCH Ở MỘT SỐ KHU VỰC NĂM 2003
(Nguồn niên giám thống kê Việt Nam 2003, NXB Thống kê, 2004)
Căn cứ bảng số liệu, cho biết nhận xét nào sau đây đúng về hoạt động du lịch ở Đông Nam Á so với Đông Á và Tây Nam Á?
A. Bình quân chi tiêu mỗi lượt khách ở Tây Nam Á cao nhất.
B. Số lượt khách du lịch ở khu vực Đông Nam Á nhiều hơn khu vực Đông Á và Tây Nam Á.
C. Tổng chi tiêu của khách du lịch khu vực Đông Á lớn hơn khu vực Đông Nam Á.
D. Hoạt động du lịch ở Đông Nam Á năm 2003 phát triển mạnh nhất so với Đông Á và Tây Nam Á.
Hướng dẫn: Qua bảng số liệu, ta thấy:
- Khách du lịch đến Đông Á đông nhất, tiếp đến là Tây Nam Á và Đông Nam Á => B, D sai.
- Chi tiêu khách du lịch Đông Á lớn nhất, tiếp đến là Tây Nam Á và Đông Nam Á => C đúng.
- Bình quân chi tiêu mỗi lượt khách ở Đông Á cao nhất => A sai.
Chọn: C
Cho bảng số liệu:
SỐ KHÁCH DU LỊCH QUỐC TẾ ĐẾN VÀ CHI TIÊU CỦA KHÁCH DU LỊCH Ở MỘT SỐ KHU VỰC NĂM 2003
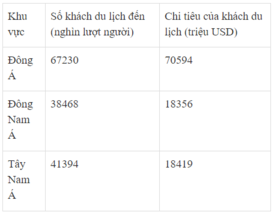
(Nguồn niên giám thống kê Việt Nam 2003, NXB Thống kê, 2004)
Căn cứ bảng số liệu, cho biết nhận xét nào đúng về hoạt động du lịch ở Đông Nam Á so với Đông Á và Tây Nam Á?
A. Bình quân chi tiêu mỗi lượt khách ở Tây Nam Á cao nhất.
B. Tổng chi tiêu của khách du lịch khu vực Đông Á lớn hơn khu vực Đông Nam Á.
C. Hoạt động du lịch ở Đông Nam Á phát triển mạnh nhất so với Đông Á và Tây Nam Á.
D. Số lượt khách du lịch ở Đông Nam Á nhiều hơn khu vực Đông Á và Tây Nam Á.
Đáp án: B
Giải thích:
- Tính bình quân chi tiêu: BQCT = chi tiêu của khách/số khách (USD/người), ta có:
Bình quân chi tiêu của các khu vực lần lượt là: Đông Á (1050 USD/người), Đông Nam Á (477,2 USD/người) và Tây Nam Á (445 USD/người). Như vậy, bình quân chi tiêu của khách du lịch đến khu vực Đông Á là cao nhất và Tây Nam Á là thấp nhất.
- Số khách du lịch đến và chi tiêu của khách du lịch khu vực Đông Á là đông, nhiều nhất. Khu vực Đông Nam Á là ít nhất.