a,  A n B ⏜ - cung lớn;  A m B ⏜ - cung nhỏ

Vì sđ A n B ⏜ + sđ A m B ⏜ =  360 0 ; mà sđ A n B ⏜ = 3sđ A m B ⏜

nên sđ A n B ⏜ =  270 0  và độ dài cung  A n B ⏜ là  l = 3 πR 2

b, Vì DOAB vuông cân =>  A O B ^ = 90 0  và O A B ^ = O B A ^ = 45 0

c, Vì AB = R 2 => OH = R 2 2 (OH ⊥ AB; H ∈ AB)

Lời giải:
a. Câu hỏi chưa rõ ràng

b. Vì số đo cung nhỏ AB bằng một nửa số đo cung lớn AB mà tổng số
 đo 2 cung bằng $360^0$ nên số đo cung nhỏ $AB$ là $120^0$

Từ $O$ kẻ $OH\perp AB$ như hình. Tam giác $OAB$ cân tại $O$ nên đường cao $OH$ đồng thời là đường phân giác, trung tuyến.
Do đó: $\widehat{AOH}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}.120^0=60^0$

$\frac{AH}{AO}=\sin \widehat{AOH}=\sin 60^0=\frac{\sqrt{3}}{2}$

$\Rightarrow AH=\frac{\sqrt{3}}{2}AO=\frac{\sqrt{3}}{2}R$

$\Rightarrow AB=2AH=\sqrt{3}R$

Hình vẽ:

a) + Dùng compa vẽ đường tròn tâm O, bán kính R = 2cm.

+ Trên đường tròn lấy điểm A.Nối OA từ đó vẽ góc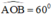 

Khi đó ta được cung AB có số đo bằng  60 º .

+ ΔAOB có OA = OB,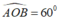

⇒ ΔAOB đều

⇒ AB = OA = OB = R = 2cm.

b) Chia đường tròn thành 6 cung bằng nhau:

+ Vẽ đường tròn tâm O, bán kính R.

+ Trên đường tròn tâm O, lấy điểm A.

+ Vẽ cung tròn tâm A, bán kính R cắt đường tròn tại B và C.

+ Vẽ cung tròn tâm B và C bán kính R cắt đường tròn tâm O tại giao điểm thứ hai là D và E.

+ Vẽ cung tròn tâm E bán kính R cắt đường tròn (O) tại giao điểm thứ hai là F.

Khi đó, ta chia được đường tròn thành sáu cung bằng nhau như trên

Từ O kẻ đg thg vg góc vs AB tại H

=> AH=BH=AB/2 = R căn 3 /2 

Theo hệ thức lượng trong tam giác AHO vuông ở H ta có 

SIN góc AOH = R căn 3 /2 : R 

                      = căn 3/2 = 60 

=> Góc AOB = 2 góc AOH= 2*60 =120

SĐ AB nhỏ =120

SĐ AB lớn = 360 - sđ AB nhỏ = 360 -120 = 240

a: Xét (O) có 

\(\widehat{AOM}=\stackrel\frown{AM}\)

\(\widehat{BOM}=\stackrel\frown{BM}\)

mà \(\widehat{AOM}=\widehat{BOM}\)

nên \(\overrightarrow{MA}=\stackrel\frown{MB}\)

R 2