Cho hình thoi ABCD có \(\widehat{A}=60^o\). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
Những câu hỏi liên quan
Cho hình thoi ABCD có A ^ = 60°. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh đa giác MBNPDQ là lục giác đều
Chứng minh được M Q = N P = 1 2 B D
Chứng minh tam giác ABD đều, suy ra được MN = BN = NP PD = DQ = QM
Chứng minh các góc của đa giác MBNPDQ bằng nhau và cùng bằng 1200.
Từ đó quy ra đa giác MBNPDQ là lục giác đều (ĐPCM).
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có \(\widehat{A}=60^0\). Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều ?
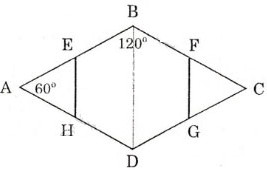
ABCD là hình thoi, 
= 
nên 
= 
, 
= .
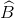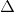EAH là tam giác đều (vì tam giác cân có một góc ) nên 
= , 
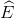= . Cũng thế 
= , 
= .
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều
Đúng 0
Bình luận (0)
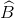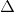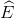ABCD là hình thoi, = nên = , = .EAH là tam giác đều (vì tam giác cân có một góc ) nên = , = . Cũng thế = , = .
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình thoi ABCD có góc ∠A = 60o. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.
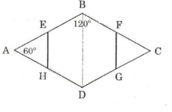
+ ABCD là hình thoi
⇒ AD // BC
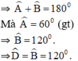
+ ABCD là hình thoi ⇒ AB = BC = CD = DA
Mà E, F, G, H là trung điểm của 4 đoạn thẳng trên
⇒ AE = EB = BF = FC = CG = GD = DH = HA.
ΔAEH có góc A = 60º và AE = AH nên là tam giác đều
+ Lại có ΔAEH đều
⇒ EH = AH = AE.
Chứng minh tương tự : FG = FC = CG
⇒ EB = BF = FG = GD = DH = HE.
Vậy EBFGDH có tất cả các góc bằng nhau và tất cả các cạnh bằng nhau nên là lục giác đều.
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có góc A = 60 độ. Gọi E, F ,G, H lần lượt la trung điểm của các cạnh AB, BC,CD,DA. Chứng minh đa giác EBFGDH là lục giác đều
Mình đang cần gấp , các bạn giúp mình với
Bạn tham khảo ở link này nha :
https://h.vn/hoi-dap/question/246529.html
~~ Hok tốt ~~
Bài giải này cùng link : https://h.vn/hoi-dap/question/246529.html nên bạn tham khảo nhé
Cho hình thang cân ABCD (AB//CD và AB<CD)
a) Gọi các điểm M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh rằng MNPQ là hình thoi.
b) Trên cạnh CD lấy điểm E sao cho CE = AB. Chứng minh rằng AC là phân giác góc BCD thì tứ giác ABCE là hình thoi.
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Gọi H, I, K, L lần lượt là hình chiếu của O trên các cạnh AB, BC, CD, DA. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC,CD,DA.a) Chứng minh rằng bốn điểm H, I, K, L cùng thuộc một đường tròn. Tính bán kính của đường tròn đó trong trường hợp AC4cm, góc A60 độb) Chứng minh rằng bốn điểm M, N, P, Q cùng thuộc một đường tròn. Khi đó, tìm điều kiện của hình thoi để hai đỉnh B, D cũng thuộc đường tròn đó.
Đọc tiếp
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Gọi H, I, K, L lần lượt là hình chiếu của O trên các cạnh AB, BC, CD, DA. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC,CD,DA.
a) Chứng minh rằng bốn điểm H, I, K, L cùng thuộc một đường tròn. Tính bán kính của đường tròn đó trong trường hợp AC=4cm, góc A=60 độ
b) Chứng minh rằng bốn điểm M, N, P, Q cùng thuộc một đường tròn. Khi đó, tìm điều kiện của hình thoi để hai đỉnh B, D cũng thuộc đường tròn đó.
Cho hình thoi ABCD có \(\widehat{D}=60^o\). E, H, G, F lần lượt là trung điểm của AB, BC, CD, DA.
a) Chứng minh tứ giác EFGH là hình chữ nhật
b) Cho AG cắt HF tại J. Chứng minh rằng HF = 4FJ
c) Gọi I là trung điểm FJ và P là giao điểm của EH và DB. Chứng minh IG vuông góc với IP.
d) Cho AB = 2cm. Tính độ dài IP
Cho hình thoi ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD ,DA. Chứng minh tứ giác MNPQ là hình chữ nhật.
Cho hình thang cân ABCD( AB//CD ). Gọi M,N,P,Q lần lượt là trung điểm các cạnh AB,BC,CD và DA. Chứng minh:
a) tam giác MCD cân
b) MP Vuông với QN
c) tứ giác MNPQ là hình thoi. Vẽ H đối xứng P qua Q, K đối xứng P qua N. Chứng minh: M là trung điểm của HK.
Xem chi tiết
19 tháng 8 2023 lúc 9:32
Bài 2: Cho hình chữ nhật ABCD có M , N , P ,Q lần lượt là trung điểm các cạnh AB , BC , CD , DA a, Chứng minh tứ giác MNPQ là hình thoi
Xét ΔABD có M,Q lần lượt là trung điểm của AB,AD
=>MQ là đường trung bình
=>MQ//BD và MQ=BD/2
Xét ΔCBDcó
N,P lần lượt là trung điểm của CB,CD
=>NP là đường trung bình
=>NP//BD và NP=BD/2
=>MQ//NP và MQ=NP
Xét ΔBAC có M,N lần lượt là trung điểm của BA,BC
=>MN là đường trung bình
=>MN=AC/2=BD/2=MQ
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
=>MNPQ là hình bình hành
mà MN=MQ
nên MNPQ là hình thoi
Đúng 0
Bình luận (0)