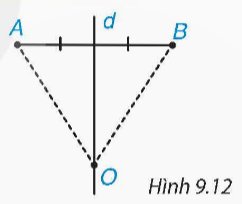
Cho d là đường trung trực của đoạn thẳng AB và O là một điểm trên d (H.9.12). Hỏi đường tròn tâm O đi qua A thì có đi qua B không?
Những câu hỏi liên quan
Cho đường thẳng d và hai điểm A, B thuộc cùng một mặt phẳng bờ d, sao cho đường thẳng AB không vuông góc với d.
a) Vẽ đường tròn tâm O đi qua hai điểm A,B sao cho O nằm trên d;
b) Gọi C, D là giao điểm của d với đường tròn tâm O kể trên. Chứng minh O nằm trên các đường trung trực các đoạn thẳng BC, AD, AC, DB, CD.
Cho đường tròn tâm O bán kính R và điểm A thuộc đường tròn. Trên tiếp tuyến tại A lấy 1 điểm K cố định. Một đường thẳng (d) thay đổi đi qua K và không đi qua tâm O cắt (O) tại B và C ( B nằm giữa C và K). Gọi M là trung điểm BC.1.CM: A,O,M,K thuộc 1 đường tròn2.Vẽ đường kính AN của đường tròn tâm O, đường thẳng qua A và vuông góc vứi BC cắt MN tại H.CM: tứ giác BHCN là hình bình hành.3.CM: H là trực tâm tam giác ABC.4. Khi đường thẳng (d) thay đổi và thỏa mãn điều kiện đề bài thì H di động trên...
Đọc tiếp
Cho đường tròn tâm O bán kính R và điểm A thuộc đường tròn. Trên tiếp tuyến tại A lấy 1 điểm K cố định. Một đường thẳng (d) thay đổi đi qua K và không đi qua tâm O cắt (O) tại B và C ( B nằm giữa C và K). Gọi M là trung điểm BC.
1.CM: A,O,M,K thuộc 1 đường tròn
2.Vẽ đường kính AN của đường tròn tâm O, đường thẳng qua A và vuông góc vứi BC cắt MN tại H.CM: tứ giác BHCN là hình bình hành.
3.CM: H là trực tâm tam giác ABC.
4. Khi đường thẳng (d) thay đổi và thỏa mãn điều kiện đề bài thì H di động trên đường thẳng nào
Ai làm giúp với =((
a) ΔOBCΔOBC có OB=OC=ROB=OC=R nên ΔOBCΔOBC cân đỉnh OO,
có OMOM là đường trung tuyến nên OMOM cũng là đường cao
⇒OM⊥CB⇒OM⊥CB
⇒ˆOMB=90o⇒OMB^=90o
Tứ giác AOMKAOMK có ˆOMK+ˆOAK=90o+90o=180oOMK^+OAK^=90o+90o=180o
Do đó AOMKAOMK nội tiếp đường tròn đường kính (OK)(OK)
b) Xét ΔAHNΔAHN có:
OM∥AHOM∥AH (vì cùng ⊥BC⊥BC)
OO là trung điểm của ANAN
⇒OM⇒OM là đường trung bình ΔAHNΔAHN
⇒M⇒M là trung điểm HNHN
Tứ giác BHCNBHCN có hai đường chéo CBCB và HNHN cắt nhau tại MM là trung điểm của mỗi đường
⇒BHCN⇒BHCN là hình bình hành.
c) Ta có ΔACNΔACN nội tiếp đường tròn (O)(O) đường kính ANAN
nên ˆACN=90o⇒CN⊥ACACN^=90o⇒CN⊥AC
Tứ giác BHCNBHCN là hình bình hành
⇒BH∥CN⇒BH∥CN mà CN⊥ACCN⊥AC
⇒BH⊥AC⇒BH⊥AC
Lại có AH⊥BCAH⊥BC
ΔABCΔABC có BHBH và CHCH là 2 đường cao cắt nhau tại HH
nên HH là trực tâm ΔABCΔABC
d) MM là trung điểm cạnh BCBC
Lấy điểm O′O′ đối xứng với OO qua MM do B,CB,C cố định suy ra MM cố đinh suy ra O′O′ cố định
Ta có: OM∥AHOM∥AH (vì vùng ⊥BC⊥BC)
⇒OO′∥AH⇒OO′∥AH,
OMOM là đường trung bình ΔAHN⇒OM=12AH⇒AH=2OM=OO′ΔAHN⇒OM=12AH⇒AH=2OM=OO′
Do đó AOO′HAOO′H là hình bình hành
⇒O′H=OA=R⇒O′H=OA=R không đổi
Dựng hình bình hành HO′KTHO′KT ta được KT∥O′HKT∥O′H và có KT=O′HKT=O′H nên TT cố định
TH=O′K=OKTH=O′K=OK
Vậy H∈(T;KO)
Cho đường tròn (O,R) và đường thẳng d không đi qua O, cắt đường tròn tại hai điểm A và B.Lấy một điểm M trên tia đối của tia BA kẻ hai tiếp tuyến MC,MD với đường tròn (C,D là tiếp điểm).Gọi H là trung điểm của AB.
a)chứng minh 4 điểm M,D,O,H cùng thuộc 1 đường tròn.
b)đoạn thẳng OM cắt đường tròn tại I.chứng minh I là tâm đương tròn nội tiếp tam giác MCD
a) zì H là trung điểm của AB nên \(OH\perp AB\)hay \(\widehat{OHM}=90^0\)
theo tính chất của tiếp tuyến ta lại có \(OD\perp DM\left(hay\right)\widehat{ODM}=90^0\)
=> M,D,O,H cùng nằm trên 1đường tròn
b) Theo tính chất tiếp tuyến ta có
MC=MD=> tam giác MDC cân tại M
=> MI là 1 đương phân giác của CMD , MẶt khác I là điểm chính giữa cung nhỏ CD nên :
\(\widehat{DCI}=\frac{1}{2}sđ\widebat{DI}=\frac{1}{2}sđ\widebat{CI}=\widehat{MCI}\)
=> CI là phân giác của góc MCD .
zậy I là tâm đường tròn nội tiếp tam giác MCD
Cho đường tròn tâm O, bán kính AB 2R. Gọi d1, d2 lần lượt là các tiếp tuyến của đường tròn O tại A và B. I là trung điểm của đoạn thẳng OA, E là điểm thay đổi trên đường tròn O sao cho E không trùng với A và B. Đường thẳng d đi qua E và vuông góc với EI, cắt 2 đường thẳng d1, d2 tại M và N.1. Chứng minh AMEI là tứ giác nội tiếp2. Chứng minh IB.NE 3.IE.NB3. Khi E thay đổi, chứng minh tích AM.BN có giá trị không đổi và tìm giá trị nhỏ nhất của diện tích tam giác MNI theo R
Đọc tiếp
Cho đường tròn tâm O, bán kính AB = 2R. Gọi d1, d2 lần lượt là các tiếp tuyến của đường tròn O tại A và B. I là trung điểm của đoạn thẳng OA, E là điểm thay đổi trên đường tròn O sao cho E không trùng với A và B. Đường thẳng d đi qua E và vuông góc với EI, cắt 2 đường thẳng d1, d2 tại M và N.
1. Chứng minh AMEI là tứ giác nội tiếp
2. Chứng minh IB.NE = 3.IE.NB
3. Khi E thay đổi, chứng minh tích AM.BN có giá trị không đổi và tìm giá trị nhỏ nhất của diện tích tam giác MNI theo R
Cho đường tròn tâm O và dây cung BC không đi qua O. Một điểm A chuyển động trên dường tròn (A khác B, C). Gọi M là trung điểm của đoạn AC, H là chân đường vuông góc hạ từ M xuống đường thẳng AB. Chứng minh rằng H nằm trên một đường tròn cố định.
Cho 3 điểm A, B, C cố định nằm trên đường thẳng d (B nằm giữa A và C). Gọi (O) là đường tròn thay đổi luôn đi qua 2 điểm B, C và có tâm O (O không nằm trên đường thẳng d). Kẻ 2 tiếp tuyến AM, AN của đường tròn (O), với M, N là 2 tiếp điểm. AO cắt MN tại H; đường thẳng AO cắt đường tròn (O) tại P và Q (P nằm giữa A và O). Gọi D là trung điểm HQ. Qua H kẻ đường thẳng vuông góc với MD cắt đường thẳng MP tại E. Chứng minh:a) P là trung điểm ME.b) Đường thẳng MN luôn đi qua một điểm cố định khi đường...
Đọc tiếp
Cho 3 điểm A, B, C cố định nằm trên đường thẳng d (B nằm giữa A và C). Gọi (O) là đường tròn thay đổi luôn đi qua 2 điểm B, C và có tâm O (O không nằm trên đường thẳng d). Kẻ 2 tiếp tuyến AM, AN của đường tròn (O), với M, N là 2 tiếp điểm. AO cắt MN tại H; đường thẳng AO cắt đường tròn (O) tại P và Q (P nằm giữa A và O). Gọi D là trung điểm HQ. Qua H kẻ đường thẳng vuông góc với MD cắt đường thẳng MP tại E. Chứng minh:
a) P là trung điểm ME.
b) Đường thẳng MN luôn đi qua một điểm cố định khi đường tròn (O) thay đổi.
Cho đường tròn (O; R) và điểm A cố định thuộc đường tròn. Trên tiếp tuyến với (O) tại A lấy một điểm K cố định. Một đường thẳng d thay đổi đi qua K và không đi qua tâm O cắt (O) tại điểm B và C (B nằm giữa C và K), Gọi M là trung điểm của BC.1) Chứng minh bốn điểm A, O, M, K cùng thuộc một đường tròn.2) Vẽ đường kính AN của đường tròn (O). Đường thẳng qua A và vuông góc với BC cắt MN tại H. Chứng minh tứ giác BHCN là hình bình hành.3) Chứng minh H là trực tâm tam giác ABC4) Khi đường thẳng d th...
Đọc tiếp
Cho đường tròn (O; R) và điểm A cố định thuộc đường tròn. Trên tiếp tuyến với (O) tại A lấy một điểm K cố định. Một đường thẳng d thay đổi đi qua K và không đi qua tâm O cắt (O) tại điểm B và C (B nằm giữa C và K), Gọi M là trung điểm của BC.
1) Chứng minh bốn điểm A, O, M, K cùng thuộc một đường tròn.
2) Vẽ đường kính AN của đường tròn (O). Đường thẳng qua A và vuông góc với BC cắt MN tại H. Chứng minh tứ giác BHCN là hình bình hành.
3) Chứng minh H là trực tâm tam giác ABC
4) Khi đường thẳng d thay đổi và thỏa mãn điều kiện của đề bài, điểm H di động trên đường nào?
Từ một điểm A nằm bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là tiếp điểm). Một đường thẳng (d) đi qua A cắt đường tròn (O) tại hai điểm D và E (d không đi qua tâm O, D nằm giữa A và E), gọi I là trung điểm của DE. BC cắt AE tại S. Qua C kẻ đường thẳng song song với AB, đường thẳng này cắt các đường thẳng BE, BD lần lượt tại M và N. CM: C là trung điểm MN.
Đọc tiếp
Từ một điểm A nằm bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là tiếp điểm). Một đường thẳng (d) đi qua A cắt đường tròn (O) tại hai điểm D và E (d không đi qua tâm O, D nằm giữa A và E), gọi I là trung điểm của DE. BC cắt AE tại S. Qua C kẻ đường thẳng song song với AB, đường thẳng này cắt các đường thẳng BE, BD lần lượt tại M và N. CM: C là trung điểm MN.
cho đường tròn tâm o đường kính ab=2r gọi d1 và d2 là các tiếp tuyến của o tại a và b i là trung điểm của đoạn thẳng oa.e là điểm thay đổi trên đường tròn tâm o đường thẳng d đi qua e và vuông góc với đường thẳng ei cắt d1 và d2 lần lượt tại m và n chứng minh tứ giác amei nội tiếp và chứng minh ib×ne=3ie×nb
góc MAI+góc MEI=180 độ
=>MAIE nội tiếp
Đúng 0
Bình luận (0)
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn (O). Qua điểm A dựng hai tiếp tuyến AM,AN đến đường tròn (O) với M,N là các tiếp điểm. Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (ABAC, đường thẳng d không đi qua tâm O)a) Chứng minh tứ giác AMON là tứ giác nội tiếpb) Chứng minh AN^2AB.ACc) Hai tiếp tuyến của đường trong (O) tại B và C cắt nhau tại K. Chứng minh rằng điểm K luôn thuộc một đường thẳng cố định khi đường thẳng d thay đổi và đường thẳng d thỏa mãn điều kiệ...
Đọc tiếp
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn (O). Qua điểm A dựng hai tiếp tuyến AM,AN đến đường tròn (O) với M,N là các tiếp điểm. Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (AB<AC, đường thẳng d không đi qua tâm O)
a) Chứng minh tứ giác AMON là tứ giác nội tiếp
b) Chứng minh AN\(^2\)=AB.AC
c) Hai tiếp tuyến của đường trong (O) tại B và C cắt nhau tại K. Chứng minh rằng điểm K luôn thuộc một đường thẳng cố định khi đường thẳng d thay đổi và đường thẳng d thỏa mãn điều kiện đề bài
a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔANB và ΔACN có
góc ANB=góc ACN
góc NAB chung
=>ΔANB đồng dạng với ΔACN
=>AN^2=AB*AC
Đúng 0
Bình luận (0)