Lập bảng tần số cho mẫu dữ liệu thu được trong HĐ1.

Những câu hỏi liên quan
Xét dữ liệu cho trong tình huống mở đầu.a) Mẫu số liệu về tổng điểm, kí hiệu là (T), có bao nhiêu giá trị?b) Nếu lập bảng tần số cho mẫu số liệu (T) thì có dễ hình dung được bức tranh tổng thể về kết quả thi không? Vì sao?c) Mẫu số liệu (T) được mô tả dưới dạng bảng thống kê sau:
Đọc tiếp
Xét dữ liệu cho trong tình huống mở đầu.
a) Mẫu số liệu về tổng điểm, kí hiệu là (T), có bao nhiêu giá trị?
b) Nếu lập bảng tần số cho mẫu số liệu (T) thì có dễ hình dung được bức tranh tổng thể về kết quả thi không? Vì sao?
c) Mẫu số liệu (T) được mô tả dưới dạng bảng thống kê sau:

a) Tổng số giá trị của mẫu số liệu là: 344 752 \( \times \) 4 = 1 379 008 giá trị.
b) Nếu lập bảng tần số cho mẫu số liệu (T) sẽ dễ hình dung được bức tranh tổng thể về kết quả thi vì giúp thuận lợi cho việc tổ chức đọc và phân tích số liệu.
c) Số lượng thí sinh có ít nhất một môn học có điểm dưới 6 là 23.
Số lượng thí sinh có ít nhất 1 môn học có điểm từ 6 đến dưới 7 là 69.
…
Số lượng thí sinh có tổng điểm 3 môn học từ 28 đến dưới 29 là 216.
Số lượng thí sinh có tổng điểm 3 môn học từ 29 đến 30 là 12.
Đúng 0
Bình luận (0)
Thống kê về các loại lồng đèn mà các bạn học sinh lớp 8C làm được để trao tặng cho trẻ em khuyết tật nhân dịp Tết trung thu được cho trong bảng dữ liệu sau:a) Tìm dữ liệu định tính và dữ liệu định lượng trong bảng dữ liệu trênb) Trong số các dữ liệu định tính tìm được, dữ liệu nào có thể so sánh hơn kém?c) Trong số các dữ liệu định lượng tìm được, dữ liệu nào là rời rạc?
Đọc tiếp
Thống kê về các loại lồng đèn mà các bạn học sinh lớp 8C làm được để trao tặng cho trẻ em khuyết tật nhân dịp Tết trung thu được cho trong bảng dữ liệu sau:
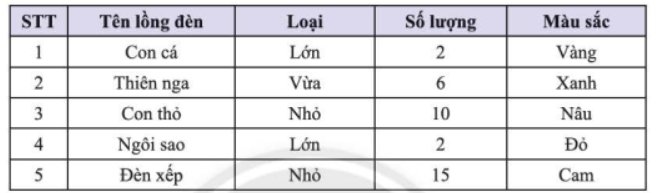
a) Tìm dữ liệu định tính và dữ liệu định lượng trong bảng dữ liệu trên
b) Trong số các dữ liệu định tính tìm được, dữ liệu nào có thể so sánh hơn kém?
c) Trong số các dữ liệu định lượng tìm được, dữ liệu nào là rời rạc?
a: ĐỊnh tính: tên lồng đèn, loại, màu sắc
Định lượng: số lượng
b: Dữ liệu có thể so sánh hơn kém: loại
c: Dữ liệu là rời rạc: số lượng
Đúng 0
Bình luận (0)
Hãy thiết lập tính năng sắp xếp và lọc dữ liệu cho bảng dữ liệu trong Hình 1 và so sánh các kết quả thu được khi lần lượt nháy chuột vào biểu tượng trên dòng tiêu đề các cột Lớp và cột Sĩ số.
Đọc tiếp
Hãy thiết lập tính năng sắp xếp và lọc dữ liệu cho bảng dữ liệu trong Hình 1 và so sánh các kết quả thu được khi lần lượt nháy chuột vào biểu tượng  trên dòng tiêu đề các cột Lớp và cột Sĩ số.
trên dòng tiêu đề các cột Lớp và cột Sĩ số.
Các bước thiết lập tính năng và lọc:
Bước 1: Nháy chuột vào một ô tính bất kì trong bảng dữ liệu cần sắp xếp hoặc lọc (ví dụ ô C10 trong Hình 1).
Bước 2: Chọn dải lệnh Data trên bảng chọn chức năng.
Bước 3: Nháy chuột vào biểu tượng Filter trong nhóm lệnh Sort & Filter.
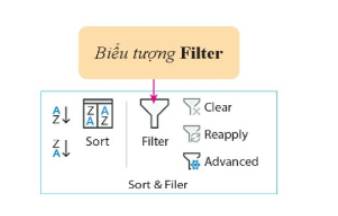
Sau Bước 3, biểu tượng ![]() sẽ xuất hiện tại cạnh bên phải các ô tiêu đề của tất cả các cột trong vùng dữ liệu. Lúc này bảng dữ liệu đã sẵn sàng cho các thao tác sắp xếp và lọc dữ liệu.
sẽ xuất hiện tại cạnh bên phải các ô tiêu đề của tất cả các cột trong vùng dữ liệu. Lúc này bảng dữ liệu đã sẵn sàng cho các thao tác sắp xếp và lọc dữ liệu.
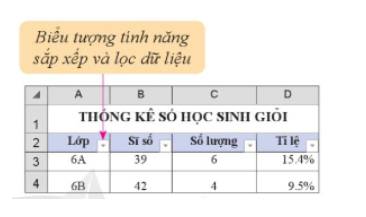
Lưu ý: Chỉ lọc các cột Lớp và cột Sĩ số.
Kết quả: Khi nháy chuột vào biểu tượng ![]() sẽ hiển thị:
sẽ hiển thị:
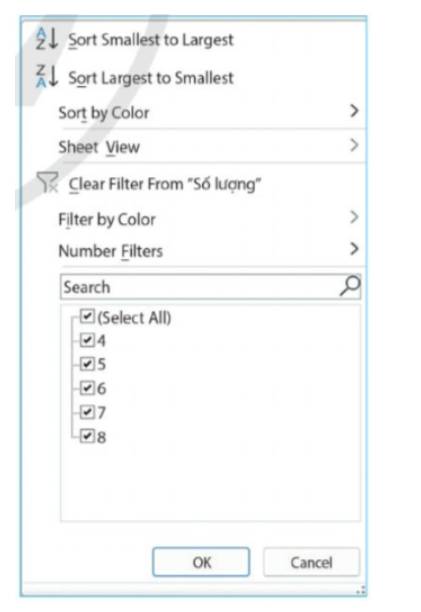
Phần mềm bảng tính hỗ trợ nhiều phương pháp lọc khác nhau: lọc giá trị hoặc lọc theo điều kiện.
Đúng 0
Bình luận (0)
Lập bảng thống kê cho ba dãy dữ liệu thu được.
| Bạn A | Bạn B | Bạn C |
(1) | 1h | 2h | 1,5h |
(2) | Phim hoạt hình, thời sự | Phim hoạt hình, Đường lên đỉnh Olympia | Quà tặng cuộc sống, Đường lên đỉnh Olympia, Doremon |
(3) | Đồng ý | Rất đồng ý | Không đồng ý |
Đúng 0
Bình luận (0)
Xếp loại học lực của học sinh tổ 1 lớp 6A được ghi lại trong bảng dữ liệu sau:
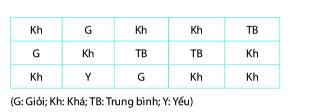
Em hãy lập bảng thống kê theo mẫu dưới đây:

Một CSDL được tạo lập bằng Access gồm những gì?
A. Bảng dữ liệu và mối liên kết giữa các bảng đó
B. Bảng dữ liệu và mối liên kết giữa các biểu mẫu đó
C. Biểu mẫu và mối liên kết giữa các bảng đó
D. Biểu mẫu và mối liên kết giữa các biểu mẫu đó
B. Bảng dữ liệu và mối liên kết giữa các biểu mẫu đó
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Thống kê điểm toán của 40 học sinh của một lớp người ta thu được mẫu số liệu ban đầu như sau: Lập bảng phân bố tần số - tần suất ghép lớp với các lớp như sau: [1; 2]; [3; 4]; [5; 6]; [7; 8]; [9; 10] Từ đó; chọn mệnh đề đúng trong các mệnh đề sau? A. Lớp 2 và 4 có cùng tần số B. Lớp 5 có tần suất cao nhất C. Lớp 3 có tần số thấp nhất D. tất cả sai
Đọc tiếp
Thống kê điểm toán của 40 học sinh của một lớp người ta thu được mẫu số liệu ban đầu như sau:
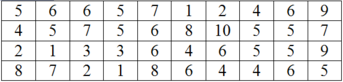
Lập bảng phân bố tần số - tần suất ghép lớp với các lớp như sau:
[1; 2]; [3; 4]; [5; 6]; [7; 8]; [9; 10]
Từ đó; chọn mệnh đề đúng trong các mệnh đề sau?
A. Lớp 2 và 4 có cùng tần số
B. Lớp 5 có tần suất cao nhất
C. Lớp 3 có tần số thấp nhất
D. tất cả sai
Chọn A.
Bảng phân bố tần số - tần suất
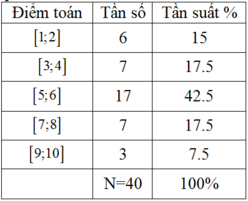
Dựa vào bảng trên ta thấy lớp 3 có tần số và tần suất cao nhất; lớp 5 có tần số; tần suất thấp nhất.
Lớp 2 và 4 có cùng tần số và tần suất.
Đúng 0
Bình luận (0)
Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau:a) Tìm tứ phân vị của dãy số liệu trên.b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:c) Hãy ước lượng tứ phân vị của số liệu từ bảng tần số ghép nhóm trên.
Đọc tiếp
Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau:

a) Tìm tứ phân vị của dãy số liệu trên.
b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
c) Hãy ước lượng tứ phân vị của số liệu từ bảng tần số ghép nhóm trên.
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right) = \frac{1}{2}\left( {11 + 11} \right) = 11\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) = \frac{1}{2}\left( {14 + 14} \right) = 14\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right) = \frac{1}{2}\left( {21 + 22} \right) = 21,5\)
b)

c) Do số trận đấu là số nguyên nên ta hiệu chỉnh như sau:

Tổng trận đấu là: \(n = 4 + 8 + 2 + 6 = 20\).
Gọi \({x_1};{x_2};...;{x_{20}}\) là điểm số của các trận đấu được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_4} \in \begin{array}{*{20}{c}}{\left[ {5,5;10,5} \right)}\end{array};{x_5},...,{x_{12}} \in \begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array};{x_{13}},{x_{14}} \in \begin{array}{*{20}{c}}{\left[ {15,5;20,5} \right)}\end{array};{x_{15}},...,{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right)\)
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_{10}},{x_{11}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}.\left( {15,5 - 10,5} \right) = 14,25\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_5},{x_6} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{4} - 4}}{8}.\left( {15,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 6;C = 4 + 8 + 2 = 14;{u_j} = 20,5;{u_{j + 1}} = 25,5\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 20,5 + \frac{{\frac{{3.20}}{4} - 14}}{6}.\left( {25,5 - 20,5} \right) \approx 21,3\)
Đúng 0
Bình luận (0)
Kết quả bài kiểm tra môn Toán của 36 học sinh được cho trong mẫu số liệu sau:a) Lập bảng phân bố tần số và tần suất ghép lớp ( chính xác đến hàng phần trăm) sử dụng 5 lớp sau: [0;2), [2;4), [4;6), [6;8), [8;10)b) Vẽ biểu đồ tần suất hình quạt thể hiện bảng phân bố ở câu a).
Đọc tiếp
Kết quả bài kiểm tra môn Toán của 36 học sinh được cho trong mẫu số liệu sau:
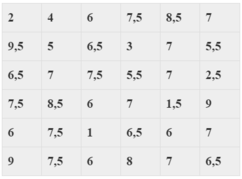
a) Lập bảng phân bố tần số và tần suất ghép lớp ( chính xác đến hàng phần trăm) sử dụng 5 lớp sau: [0;2), [2;4), [4;6), [6;8), [8;10)
b) Vẽ biểu đồ tần suất hình quạt thể hiện bảng phân bố ở câu a).
a) Lập bảng phân bố tần số và tần suất ghép lớp ( chính xác đến hàng phần trăm) sử dụng 5 lớp sau: [0;2), [2;4), [4;6), [6;8), [8;10)
| Lớp | Tần số | Tần suất |
|---|---|---|
| [0;2) | 2 | 5,56% |
| [2;4) | 3 | 8,33% |
| [4;6) | 4 | 11,11% |
| [6;8) | 21 | 58,33% |
| [8;10) | 6 | 16,67% |
| N = 36 | 100% |
b) Vẽ biểu đồ tần suất hình quạt thể hiện bảng phân bố ở câu a).
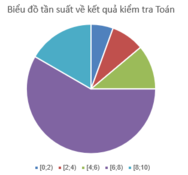
Đúng 0
Bình luận (0)
Thống kê số huy chương bốn quốc gia dẫn đầu SEA Games 31 được cho trong bảng số liệu sau:Hãy chuyển dữ liệu đã cho vào bảng thống kê theo mẫu dưới đây và vào biểu đồ cột kép tương ứng.
Đọc tiếp
Thống kê số huy chương bốn quốc gia dẫn đầu SEA Games 31 được cho trong bảng số liệu sau:
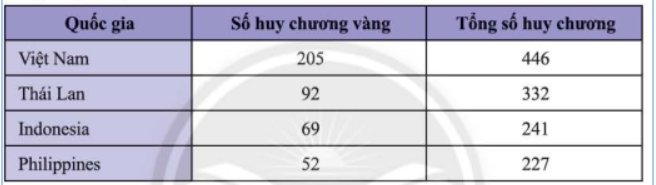
Hãy chuyển dữ liệu đã cho vào bảng thống kê theo mẫu dưới đây và vào biểu đồ cột kép tương ứng.

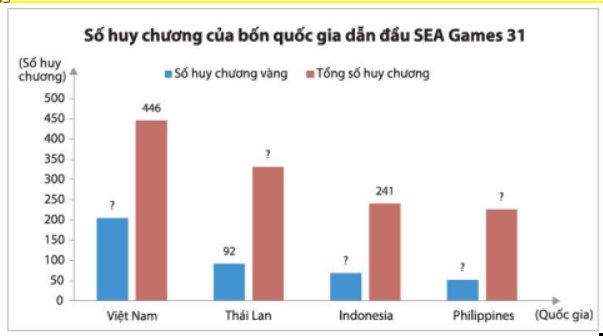
Điền số vào bảng: 446 92 69 227
Biểu đồ; 205 322 69 52 227
Đúng 0
Bình luận (0)


















