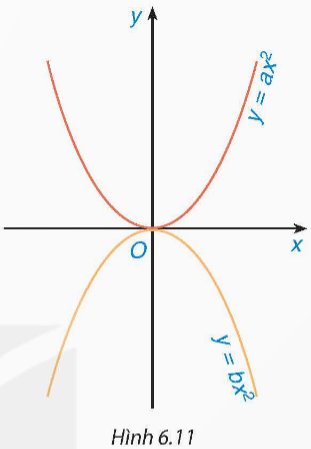
Hình 6.11 là hai đường parabol trong mặt phẳng toạ độ Oxy. Khẳng định nào sau đây là đúng?
A. a < 0 < b. B. a < b < 0.
C. a > b > 0. D. a > 0 > b.
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho đường tròn
(
C
)
:
x
2
+
y
2
-
4
x
+
2
y
-
7
0
và hai điểm A(1;1) và B(-1;2). Khẳng định nào dưới đây là đúng? A. A nằm trong và B nằm ngoài (C). B. A và B cùng nằm ngoài (C). C. A nằm ngoài và B nằm trong (C). D. A và B cùng nằm trong (C)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn ( C ) : x 2 + y 2 - 4 x + 2 y - 7 = 0 và hai điểm A(1;1) và B(-1;2). Khẳng định nào dưới đây là đúng?
A. A nằm trong và B nằm ngoài (C).
B. A và B cùng nằm ngoài (C).
C. A nằm ngoài và B nằm trong (C).
D. A và B cùng nằm trong (C)
Trong mặt phẳng tọa độ Oxy, cho bốn điểm A( 7; -3); B( 8; 4); C ( 1; 5) và D(0; -2). Khẳng định nào sau đây đúng? A.
A
C
→
⊥
C
B
→
.
B. Tam giác ABC đều. C. Tứ giác ABCD là hình vuông. D. Tứ giác ABCD không nội tiếp đường tròn.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho bốn điểm A( 7; -3); B( 8; 4); C ( 1; 5) và D(0; -2). Khẳng định nào sau đây đúng?
A. A C → ⊥ C B → .
B. Tam giác ABC đều.
C. Tứ giác ABCD là hình vuông.
D. Tứ giác ABCD không nội tiếp đường tròn.
Ta có
A B → = 1 ; 7 ⇒ A B = 1 2 + 7 2 = 5 2 B C → = − 7 ; 1 ⇒ B C = 5 2 C D → = − 1 ; − 7 ⇒ C D = 5 2 D A → = 7 ; − 1 ⇒ D A = 5 2 ⇒ A B = B C = C D = D A = 5 2 .
Lại có: A B → . B C → = 1 − 7 + 7.1 = 0 nên A B ⊥ B C .
Từ đó suy ra ABCD là hình vuông.
Chọn C.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho A(-1; -1) ; B(3; 1) và C(6; 0). Khẳng định nào sau đây đúng. A.
A
B
→
-
4
;
-
2
B.
B
^
135
°
C. AB 13 D. BC 3
Đọc tiếp
Trong mặt phẳng Oxy cho A(-1; -1) ; B(3; 1) và C(6; 0). Khẳng định nào sau đây đúng.
A. A B → - 4 ; - 2
B. B ^ = 135 °
C. AB = 13
D. BC = 3
Chọn B.
Xét các phương án:
Phương án A: do 
nên loại A
Phương án B:
Ta có 
suy ra
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;4;1), B(-1;1;3) và mặt phẳng (P):x-3y+2z-50 Một mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có dạng ax+by+cz-110 Khẳng định nào sau đây là đúng? A. a+bc B. a+b+c 5 C. a ϵ (b;c) D. a+b c
Đọc tiếp
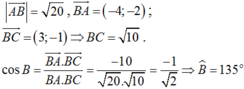
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;4;1), B(-1;1;3) và mặt phẳng (P):x-3y+2z-5=0 Một mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có dạng ax+by+cz-11=0 Khẳng định nào sau đây là đúng?
A. a+b=c
B. a+b+c = 5
C. a ϵ (b;c)
D. a+b > c
Trong mặt phẳng tọa độ Oxy cho hình bình hành OABC, C nằm trên Ox. Khẳng định nào sau đây đúng ?
a) \(\overrightarrow{AB}\) có tung độ khác 0
b) A và B có tung độ khác nhau
c) C có hoành độ bằng 0
d) \(x_A+x_C-x_B=0\)
Cho đường thẳng
d
:
x
1
y
1
+
t
z...
Đọc tiếp
Cho đường thẳng
d : x = 1 y = 1 + t z = - 1 + t
và hai mặt phẳng: (P): x - y + z + 1 = 0 và (Q): 2x + y - z - 4 = 0
Khẳng định nào sau đây là đúng?
A. d // (P) B. d // (Q)
C. d = (P) ∩ (Q) D. d ⊥ (P).
Chọn C.
Đường thẳng d có điểm chung M(1; 1; -1) với cả hai mặt phẳng (P), (Q) và d có vectơ chỉ phương (0; 1; 1) vuông góc với cả hai vectơ pháp tuyến của (P), (Q), do đó d nằm trên cả hai mặt phẳng (P), (Q). Suy ra d = (P) ∩ (Q).
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, các khẳng định sau đúng hay sai?a, Hai vecto đối nhau thì chúng có hoành độ đối nhau.b, Vecto a→ ≠ 0→ cùng phương với vecto i→ nếu a→ có hoành độ bằng 0.c, Vecto a→ có hoành độ bằng 0 thì cùng phương với vecta j→
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, các khẳng định sau đúng hay sai?
a, Hai vecto đối nhau thì chúng có hoành độ đối nhau.
b, Vecto a→ ≠ 0→ cùng phương với vecto i→ nếu a→ có hoành độ bằng 0.
c, Vecto a→ có hoành độ bằng 0 thì cùng phương với vecta j→
a) Đúng.
Hai vec tơ đối nhau thì chúng có hoành độ đối nhau và tung độ đối nhau.
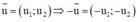
b) Sai.
Sửa lại: Vec tơ a→ cùng phương với vec tơ i→ nếu a→ có tung độ bằng 0.
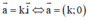
c) Đúng.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, hình lăng trụ có diện tích đáy bằng 5 (đvdt) và hai đáy là hai tam giác nằm trên hai mặt phẳng
α
,
β
có phương trình lần lượt là
α
:
x
−
2
y
+
3
z
−
a
0
và
β
:
3
x
−
6
y
+
9
z...
Đọc tiếp
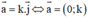
Trong không gian với hệ tọa độ Oxyz, hình lăng trụ có diện tích đáy bằng 5 (đvdt) và hai đáy là hai tam giác nằm trên hai mặt phẳng α , β có phương trình lần lượt là α : x − 2 y + 3 z − a = 0 và β : 3 x − 6 y + 9 z + b = 0 ( a , b ∈ ℝ + , b ≠ 3 a ) . Hỏi nếu thể tích khối lăng trụ bằng 5 14 thì khẳng định nào sau đây là đúng?
A. 3 a + b = 14
B. a + b 3 = 42
C. 3 a + b = 14
D. a + b 3 = 14
Trong không gian với hệ tọa độ Oxyz, hình lăng trụ có diện tích đáy bằng 5 (đvdt) và hai đáy là hai tam giác nằm trên hai mặt phẳng
α
,
β
có phương trình lần lượt là
α
:
x
−
2
y
+
3
z
−
a
0
và
β
:
3
x
−
6
y...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, hình lăng trụ có diện tích đáy bằng 5 (đvdt) và hai đáy là hai tam giác nằm trên hai mặt phẳng α , β có phương trình lần lượt là α : x − 2 y + 3 z − a = 0 và β : 3 x − 6 y + 9 z + b = 0 ( a , b ∈ ℝ + , b ≠ 3 a ) . Hỏi nếu thể tích khối lăng trụ bằng 5 14 thì khẳng định nào sau đây là đúng?
A. 3 a + b = 14
B. a + b 3 = 42
C. 3 a + b = 14
D. a + b 3 = 14
Đáp án D
Ta có
α : x − 2 y + 3 z − a = 0 ⇔ 3 x − 6 y + 9 z − 3 a = 0.
Gọi h là chiều cao của hình lăng trụ, do α / / β nên h = d α ; β = b + 3 a 3 14 .
Ta có
V = S . h ⇔ 5 14 = 5. b + 3 a 3 14 = 3 a + b = 42 ⇔ a + b 3 = 14
Đúng 0
Bình luận (0)
cho a, b là hai số nguyên trái dấu, khẳng định nào sau đây là đúng?
A. ab > 0
B. ab < 0
C. a+b > 0
D. a.b = 0
giúp mình với ạ mai mình thi rồi ạ!
Ta có: ( Giải chi tiết )
Giả sử có \(-a\) và \(b\) thì:
\(\left(-a\right).b\) ( Vì " - " nhân " + " bằng " - " \(\Rightarrow\left(-\right)< 0\)) \(\Rightarrow\) Loại A.
\(\left(-a\right).b\) ( Như trên ) \(\Rightarrow\) Giữ B.
\(\left(-a\right)+b\).
TH1: (-a) + b = -c ⇒ -c < 0. vd: (-3) + 2 = -1 < 0
TH2: (-a) + b = c ⇒ c > 0. vd: (-1) + 2 = 1 > 0
\(\Rightarrow\) Loại C.
\(\left(-a\right).b\) ( Như trường hợp a,b ) \(\Rightarrow\) Loại D.
Vậy chọn phương án B.
Đúng 0
Bình luận (0)