Tính: a) \(\sqrt[3]{125}\); b) \(\sqrt[3]{0,008}\); c) \(\sqrt[3]{\dfrac{-8}{27}}\).

Những câu hỏi liên quan
tính giá trị của biểu thức
\(A=\sqrt[3]{3+\sqrt{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt{9}+\frac{125}{7}}\)
Tính: \(\sqrt[3]{3+\sqrt{9+\frac{125}{27}}+\sqrt[3]{3-\sqrt{9+\frac{125}{27}}}}\)
Tính \(x=\sqrt[3]{3+\sqrt{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt{9+\frac{125}{27}}}\)
CMR x là số nguyên
Thực hiện phép tính rút gọn sau:
\(A=\sqrt{8}-2\sqrt{18}+3\sqrt{50}\)
\(B=\sqrt{125}-10\sqrt{\dfrac{1}{20}}-\dfrac{\sqrt{5}-5}{\sqrt{5}}\)
\(C=\dfrac{1}{\sqrt{3}+\sqrt{2}}+\sqrt{7-4\sqrt{3}}+\sqrt{2}\)
a: Ta có: \(A=\sqrt{8}-2\sqrt{18}+3\sqrt{50}\)
\(=2\sqrt{2}-6\sqrt{2}+15\sqrt{2}\)
\(=11\sqrt{2}\)
b: Ta có: \(B=\sqrt{125}-10\sqrt{\dfrac{1}{20}}+\dfrac{5-\sqrt{5}}{\sqrt{5}}\)
\(=5\sqrt{5}-\sqrt{5}+\sqrt{5}-1\)
\(=5\sqrt{5}-1\)
Đúng 1
Bình luận (0)
Tính
a) \(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}\)
b) \(\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}\)
a) 3\(\sqrt{ }\)27 – 3\(\sqrt{ }\)-8 – 3\(\sqrt{ }\)125 = 3\(\sqrt{ }\)33 – 3\(\sqrt{ }\)(-2)3 – 3\(\sqrt{ }\)53 = 3 – (-2) – 5 = 0
b) = \(\sqrt{ }\)27 – 3\(\sqrt{ }\)216 = 3\(\sqrt{ }\)33 – 3\(\sqrt{ }\)(6)3 = 3 – 6 = -3
Đúng 0
Bình luận (0)
giúp em với ạ tính
\(\sqrt[3]{125}.\sqrt[3]{\dfrac{16}{10}}.\sqrt[3]{-0,5}\)
\(\sqrt[3]{125}\cdot\sqrt[3]{\dfrac{16}{10}}\cdot\sqrt[3]{-0.5}\)
\(=\sqrt[3]{125\cdot\dfrac{16}{10}\cdot\dfrac{-1}{2}}\)
\(=\sqrt[3]{-100}\)
Đúng 2
Bình luận (1)
\(=\sqrt[3]{125.\dfrac{16}{10}.\left(-0,5\right)}\)
\(=\sqrt[3]{-100}\)
Đúng 1
Bình luận (1)
Trắc nghiệm Câu1: Kết quả phép tính sqrt{left(2+sqrt{3}right)}^2+sqrt{3} là: A.-2 B.2-2√3 C.2 D.2+2√3Câu 2: Giá trị của x để sqrt{x}-10 là: A. 5 B. 125 C. 1 D.25 Câu3 : Kết quả phép tính left(sqrt{3}+2right)left(sqrt{3-2}right) là : A.-1 B.5 C.1 D. -5Câu 5 : Cho biết sqrt{x^21}.Giá trị x là: A. x1 B. x -1 C. x_+1 D. x2giải giúp mk vớiiiiiii ạ
Đọc tiếp
Trắc nghiệm
Câu1: Kết quả phép tính \(\sqrt{\left(2+\sqrt{3}\right)}^2+\sqrt{3}\) là: A.-2 B.2-2√3 C.2 D.2+2√3
Câu 2: Giá trị của x để \(\sqrt{x}-1=0\) là: A. 5 B. 125 C. 1 D.25
Câu3 : Kết quả phép tính \(\left(\sqrt{3}+2\right)\left(\sqrt{3-2}\right)\) là : A.-1 B.5 C.1 D. -5
Câu 5 : Cho biết \(\sqrt{x^2=1}\).Giá trị x là: A. x=1 B. x= -1 C. x=_+1 D. x=2
giải giúp mk vớiiiiiii ạ
Tính:
a)\(\sqrt[3]{125}.\sqrt[3]{\dfrac{16}{10}}.\sqrt[3]{-0,5}\)
b) \(\dfrac{\sqrt[3]{4}+\sqrt[3]{2}+2}{\sqrt[3]{4}+\sqrt[3]{2}+1}\)
c) \(\sqrt{3}+\sqrt[3]{10+6\sqrt{3}}\)
d) \(\dfrac{4+2\sqrt{3}}{\sqrt[3]{10+6\sqrt{3}}}\)
e) E=\(\sqrt[3]{2+10\sqrt{\dfrac{1}{27}}}+\sqrt[3]{2-10\sqrt{\dfrac{1}{27}}}\)
a.
\(\sqrt[3]{125}.\sqrt[3]{\frac{16}{10}}.\sqrt[3]{-0,5}=\sqrt[3]{125.\frac{16}{10}.(-0,5)}=\sqrt[3]{-100}\)
b.
\(=1+\frac{1}{\sqrt[3]{4}+\sqrt[3]{2}+1}=1+\frac{\sqrt[3]{2}-1}{(\sqrt[3]{2}-1)(\sqrt[3]{4}+\sqrt[3]{2}+1)}=1+\frac{\sqrt[3]{2}-1}{(\sqrt[3]{2})^3-1}=1+\sqrt[3]{2}-1=\sqrt[3]{2}\)
c.
\(\sqrt{3}+\sqrt[3]{10+6\sqrt{3}}=\sqrt{3}+\sqrt[3]{(\sqrt{3}+1)^3}=\sqrt{3}+\sqrt{3}+1=2\sqrt{3}+1\)
Đúng 1
Bình luận (0)
d.
\(\frac{4+2\sqrt{3}}{\sqrt[3]{10+6\sqrt{3}}}=\frac{(\sqrt{3}+1)^2}{\sqrt[3]{(\sqrt{3}+1)^3}}=\frac{(\sqrt{3}+1)^2}{\sqrt{3}+1}=\sqrt{3}+1\)
e.
Đặt \(\sqrt[3]{2+10\sqrt{\frac{1}{27}}}=a; \sqrt[3]{2-10\sqrt{\frac{1}{27}}}=b\)
Khi đó:
$a^3+b^3=4$
$ab=\frac{2}{3}$
$E^3=(a+b)^3=a^3+b^3+3ab(a+b)$
$E^3=4+2E$
$E^3-2E-4=0$
$E^2(E-2)+2E(E-2)+2(E-2)=0$
$(E-2)(E^2+2E+2)=0$
Dễ thấy $E^2+2E+2>0$ nên $E-2=0$
$\Leftrightarrow E=2$
Đúng 1
Bình luận (0)
tính:
\(2\sqrt{5}\)+\(\dfrac{3}{4}\sqrt{80}\)-0,3\(\sqrt{500}\)-\(\dfrac{1}{5}\sqrt{125}\)
\(=2\sqrt{5}+3\sqrt{5}-3\sqrt{5}-\sqrt{5}=\sqrt{5}\)
Đúng 2
Bình luận (0)
Tính:
\(R=\dfrac{2}{\sqrt{4-3\sqrt[4]{5}+2\sqrt[4]{25}-\sqrt[4]{125}}}\)
Bài này nằm trong cuốn nâng cao và phát triển của Vũ Hữu Bình, và lời giải của nó thực sự rất "ảo". Có lẽ trừ tác giả ra, khó ai mà nghĩ được ra cách giải:
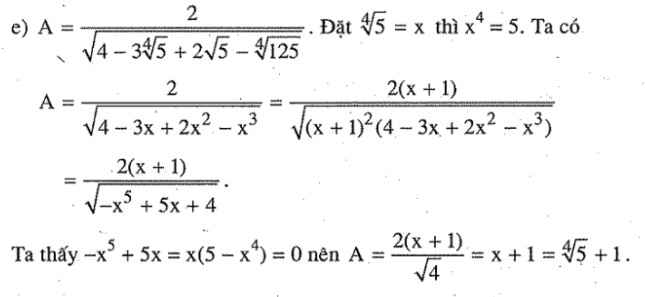
Đúng 2
Bình luận (0)























