a) Hình 80 mô tả một phần bản vẽ của chi tiết máy. Hình đó giới hạn bởi mấy đường tròn cùng tâm?
b) Hãy vẽ một hình tương tự Hình 80 bằng cách vẽ các đường tròn (O; 2 cm) và (O; 3 cm). Tính hiệu diện tích của hai hình tròn đó.
Cho nửa đường tròn đường kính AB = 4 5 . Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hia điểm cách nhau 4cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay xung quanh trục AB. Thể tích của khối tròn xoay thu được bằng:
A. V = π 5 800 5 - 928 c m 3
B. V = π 15 800 5 - 928 c m 3
C. V = π 3 800 5 - 928 c m 3
D. V = π 15 800 5 - 464 c m 3
Đáp án B.
Phương pháp: Ứng dụng tích phân để tính thể tích khối tròn xoay.
Cách giải: Gắn hệ trục tọa độ Oxy như hình vẽ:
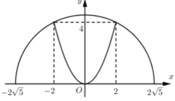
Ta có:
Phương trình đường tròn: ![]()
Phương trình parabol: ![]()
Thể tích khối cầu 
Thể tích khi quay phần tô đậm quanh trục Ox là: 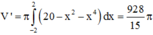
=> Thể tích cần tính 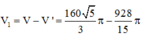
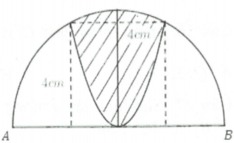
Cho nửa đường tròn đường kính A B = 4 5 . Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hai điểm cách nhau 4 cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4 cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay quanh trục AB. Thể tích của khối tròn xoay thu được bằng:
A. V = π 15 800 5 - 464 c m 3
B. V = π 3 800 5 - 928 c m 3
C. V = π 5 800 5 - 928 c m 3
D. V = π 15 800 5 - 928 c m 3
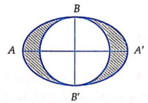
Trong mặt phẳng (P), cho elip (E) có độ dài trục lớn AA’=8 và độ dài trục nhỏ là BB’=6. Đường tròn tâm O đường kính BB’ như hình vẽ. Tính thể tích vật thể tròn xoay có được bằng cách cho miền hình phẳng giới hạn bởi đường elip và đường tròn đó (phần hình phẳng tô đậm trên hình vẽ) quay xung quanh trục AA’
A. V = 36 π
B. V = 12 π
C. V = 16 π
D. V = 64 π 3 .
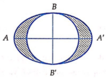
Trong mặt phẳng (P), cho elip (E) có độ dài trục lớn AA'=8 và độ dài trục nhỏ là BB'=6. Đường tròn tâm O đường kính BB’ như hình vẽ. Tính thể tích vật thể tròn xoay có được bằng cách cho miền hình phẳng giới hạn bởi đường elip và đường tròn đó (phần hình phẳng tô đậm trên hình vẽ) quay xung quanh trục AA’
A. V = 36 π
B. V = 12 π
C. V = 16 π
D. V = 64 π 3 .
Đáp án B
Thể tích của khối tròn xoay thu được khi quay elip có trục lớn A A ' = 8 , trục nhỏ B B ' = 6 khi quay quanh trục AA’ là V E = 4 3 π . A A ' 2 . B B ' 2 2 = 4 3 π .4.3 2 = 48 π (đvtt).
Thể tích khối tròn xoay thu được khi quay đường tròn O ; B B ' 2 quanh trục AA’ cũng chính là thể tích khối cầu tâm O, bán kính R = 3 . Thể tích đó là
V O ; 3 = 4 3 π R 3 = 4 3 π .3 3 = 36 π (đvtt).
Vậy thể tích khối tròn xoay cần tính là V = V E − V O ; 3 = 48 π − 36 π = 12 π (đvtt)
Hình 9.1 mô tả bản vẽ của một chi tiết. Em hãy cho biết các bước để gia công chi tiết đó. Biết rằng phôi hình trụ có đường kính 25mm dài 40mm.
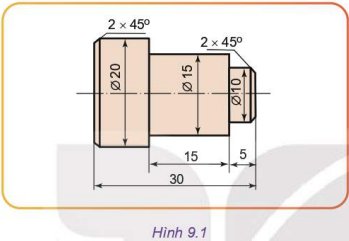
- Bước 1: Tìm hiểu chi tiết cần gia công sản xuất (hình trụ có đường kính 25 mm dài 40 mm)
- Bước 2: Chọn phôi và phương pháp chế tạo phôi (chọn phôi đảm bảo tiêu chuẩn cần được sử dụng)
- Bước 3: Xác định trình tự các bước chi tiết
Trong mặt phẳng, cho đường elip (E) có độ dài trục lớn là AA’=10, độ dài trục nhỏ là BB’=6, đường tròn tâm O có đường kính là BB’ (như hình vẽ bên dưới). Tính thể tích V của khối tròn xoay có được bằng cách cho miền hình hình phẳng giới hạn bởi đường elip và được tròn (được tô đậm trên hình vẽ) quay xung quanh trục AA’
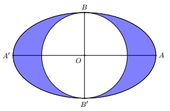
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho một hình nón đỉnh S, có đáy là hình tròn (P;PC) bị cắt bởi hai mặt phẳng song song với đáy, thiết diện lần lượt là hình tròn (M;MA), (N;NB), AM = 3cm, BN = xcm, CP = 9cm (xem hình vẽ). Biết hình giới hạn bởi hình nón, đường tròn (M;MA) và đường tròn (N;NB) có thể tích bằng hình giới hạn bởi hình nón, đường tròn (P;PC) và đường tròn (N;NB). Khi đó x bằng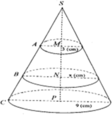
![]()
![]()
![]()
![]()
Cho (H) là hình phẳng giới hạn bởi đường thẳng d và nửa đường tròn y = 2 - x 2 biết d đi qua A - 2 ; 0 và B(1;1) trênnửa đường tròn (phần tô đậm trong hình vẽ). Diện tích của bằng:
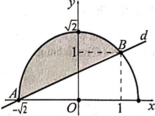
A. 3 π - 2 2 4 .
B. 3 π + 2 2 4 .
C. π - 2 2 4 .
D. π - 2 2 4 .
vẽ hai hình tròn có cùng tâm O , đường kính hình tròn lớn bằng 8cm và gấp 2 lần đường kính của hình tròn bé.Tính diện tích phần tô sọc trong hình vẽ
- Bán kính hình tròn lớn là: 8:2=4
- Diện tích hình tròn lớn là: 4x4x3,14=50,24
- Bán kính hình tròn bé là:8:2:2=2
-Diện tích hình tròn bé là: 2x2x3.14=12,56
-Diện tích phần tô sọc là: 50,24-12,56=37,68
Giải chi tiết hộ mk(k vẽ hình cx đc )
Cho đường tròn tâm O bán kính R và đường thẳng d cố định không giao nhau.từ điểm M thuộc d kẻ hai tiếp tuyến MA,MB với đường tròn(o;R).
a)Gọi I là giao điểm của Mo và cung nhỏ AB.Chứng minh rằng I là tâm đường tròn nội tiếp tam giác MAB
b)Cho biết M=r căn 3 tính diện tích phần hình phẳng bị giới hạn bởi hai tiếp tuyến MA MB và cung nhỏ AB của đường tròn
c)Chứng minh rằng khi M thay đỏi trên d thì đường thẳn AB luôn đi qua một đểm cố định.
Lười quá, chắc mình giải câu c thôi ha.
Vẽ \(OH\) vuông góc \(d\) tại \(H\). \(AB\) cắt \(OH\) tại \(L\). \(OM\) cắt \(AB\) tại \(T\)
.
CM được \(OL.OH=OT.OM=R^2\) nên \(L\) cố định. Vậy \(AB\) luôn qua \(L\) cố định.