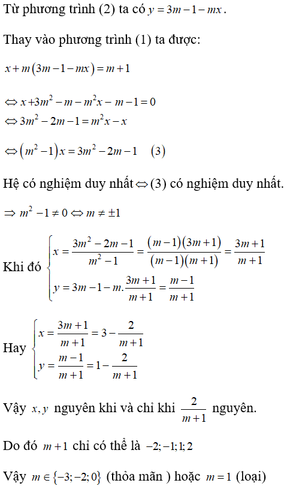Tìm số nguyên m để: /3m-1/<3

Những câu hỏi liên quan
tìm m,n nguyên dương để 3m-1/2n và 3n-1/2m cùng là số nguyên dương
Tìm m nguyên để 3m^3 + 2m^2 + 3m + 2 là một số chính phương.
Cho hệ phương trình:
x
+
m
y
m
+
1
1
m
x
+
y
3
m
-...
Đọc tiếp
Cho hệ phương trình: x + m y = m + 1 1 m x + y = 3 m - 1 2 Tìm số nguyên m để hệ phương trình có nghiệm duy nhất (x; y) mà x, y đều là số nguyên.
A. m ∈ {-3; -2}
B. m ∈ {-3; -2; 0; 1}
C. m ∈ {-3; -2; 0}
D. m = -3
(m-1) x -my =3m - 1
2x - y = m + 5
Tìm các số nguyên M để hpt có nghiệm duy nhất (x, y) là các số nguyên dương
\(\left(2\right)\Rightarrow y=2x-m-5.\)
\(\left(1\right)\Rightarrow\left(m-1\right)x-m\left(2x-m-5\right)=3m-1.\)
\(\left(m+1\right)x=m^2+2m+1.\)
Để HPT có nghiệm duy nhất => m +1 \(\ne\)0 hay m \(\ne\)-1
=>\(x=m+1>0\Rightarrow m>-1\)
=> y =2( m+1) -m -5 =m -3 > 0 => m> 3
Suy ra số nguyên m > 3 thỏa mãn
Đúng 0
Bình luận (0)
Tìm số các giá trị nguyên của tham số
m
∈
(
-
∞
;
+
∞
)
để hàm số
y
(
2
m
-
1
)
x
-
(
3
m
+...
Đọc tiếp
Tìm số các giá trị nguyên của tham số m ∈ ( - ∞ ; + ∞ ) để hàm số y = ( 2 m - 1 ) x - ( 3 m + 2 ) cos x nghịch biến trên ℝ .
A. 3
B. 4
C. 4014
D. 218
Cho A= (- vô cực;10),B=2[m;3m+1] tìm giá trị tham số m để tập hợp A giao B có đúng 3 số nguyên
Để B tồn tại \(\Leftrightarrow2m< 3m+1\Leftrightarrow m>-1\)
TH1: \(10\le3m+1\) \(\Leftrightarrow m\ge3\)
\(A\cap B=[2m;10)\) có đúng ba số nguyên khi \(6< 2m\le7\) \(\Leftrightarrow3< m\le\dfrac{7}{2}\) ( tm đk )
TH2: \(3m+1< 10\) \(\Leftrightarrow m< 3\)
\(A\cap B=\left[2m;3m+1\right]\) có đúng ba số nguyên khi
Trường hợp m nguyên thì \(2m+2=3m+1\Leftrightarrow m=1\) (thỏa mãn)
Trường hợp m là số thực thì rộng lắm...
Đúng 1
Bình luận (0)
Tìm m nguyên để 3m3 + 2m2 + 3m + 2 là một số chính phương.
Bài 6: Cho phương trình m2(x – m) x – 3m + 2 (*)a, Tìm m để (*) là phương trình bậc nhất một ẩnb, Giải PT khi m 0c, Tìm m để (1) có nghiệm x 3d, Tìm m nguyên để x nguyên
Đọc tiếp
Bài 6: Cho phương trình m2(x – m) = x – 3m + 2 (*)
a, Tìm m để (*) là phương trình bậc nhất một ẩn
b, Giải PT khi m = 0
c, Tìm m để (1) có nghiệm x = 3
d, Tìm m nguyên để x nguyên
a: =>m^2x-m^3-x+3m-2=0
=>x(m^2-1)=m^3-3m+2
=>x(m-1)(m+1)=m^3-m-2m+2=m(m-1)(m+1)-2(m-1)=(m-1)^2*(m+2)
Để đây là pt bậc nhất 1 ẩn thì (m-1)(m+1)<>0
=>m<>1 và m<>-1
b: Khi m=0 thì pt sẽ là x+2=0
=>x=-2
c: Khi x=3 thì pt sẽ là:
3(m^2-1)=m^3-3m+2
=>(m-1)^2(m+1)-3(m-1)(m+1)=0
=>(m-1)(m+1)(m-1-3)=0
=>(m-1)(m+1)(m-4)=0
=>\(m\in\left\{1;-1;4\right\}\)
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của m để A=\(\frac{m-2}{4}+\frac{3m+1}{3}\)là số nguyên âm.