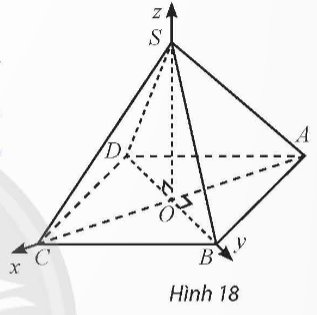
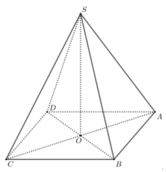
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng \(a\sqrt{2}\), chiều cao bằng 2a và O là tâm của đáy. Bằng cách thiết lập hệ trục tọa độ Oxyz như Hình 18, tính khoảng cách từ điểm C đến mặt phẳng (SAB).
Những câu hỏi liên quan
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng
a
2
. Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên theo a.
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng a 2 . Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên theo a.
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng
a
2
.
Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên theo a. A.
d
a
5
2
B.
d
a
3
2
C.
d
2
a...
Đọc tiếp
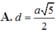
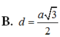
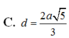
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng a 2 . Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên theo a.
A. d = a 5 2
B. d = a 3 2
C. d = 2 a 5 3
D. d = a 2 3
Chọn D.
Phương pháp:
Xác định khoảng cách từ O đến 1 mặt bên của hình chóp và sử dụng các hệ thức lượng trong tam giác vuông để làm bài toán.
Cách giải:
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO a. Khoảng cách từ O đến mặt phẳng (SCD) bằng A.
2
a
2
B.
3
a C.
5
a
5
D.
6...
Đọc tiếp
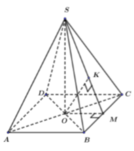
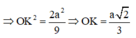
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO = a. Khoảng cách từ O đến mặt phẳng (SCD) bằng
A. 2 a 2
B. 3 a
C. 5 a 5
D. 6 a 3
Chọn A
Vẽ OE vuông góc CD, vẽ OH vuông góc với DE
Ta có
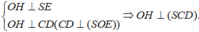
Tam giác vuông cân tại O, có
SO = OE = a
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO a. Khoảng cách từ O đến mặt phẳng (SCD) bằng A.
3
a
B.
5
a
5
C.
6
a
3
D.
2
a
2
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO = a. Khoảng cách từ O đến mặt phẳng (SCD) bằng
A. 3 a
B. 5 a 5
C. 6 a 3
D. 2 a 2
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SOa (tham khảo hình vẽ bên). Khoảng cách từ O đến mặt phẳng (SCD) bằng A.
a
3
B.
a
5
5
C.
a
6
3
D.
a
2
2
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO=a (tham khảo hình vẽ bên). Khoảng cách từ O đến mặt phẳng (SCD) bằng
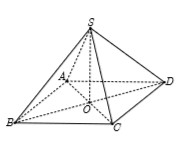
A. a 3
B. a 5 5
C. a 6 3
D. a 2 2
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO a (tham khảo hình vẽ bên)Khoảng cách từ O đến mặt phẳng (SCD) bằng A.
2
a
2
B.
3
a
C.
5
a
5
D.
6...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO = a (tham khảo hình vẽ bên)
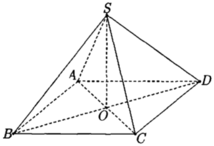
Khoảng cách từ O đến mặt phẳng (SCD) bằng
A. 2 a 2
B. 3 a
C. 5 a 5
D. 6 a 3
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SOa (tham khảo hình vẽ bên). Khoảng cách từ O đến mặt phẳng (SCD) bằng
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO=a (tham khảo hình vẽ bên). Khoảng cách từ O đến mặt phẳng (SCD) bằng
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O cạnh 2a. Thể tích khối chóp S.ABCD bằng
4
a
3
.
Tính khoảng cách từ điểm O tới mặt bên của hình chóp. A.
a
2
2
B.
3
a
4
C.
3
a
10...
Đọc tiếp
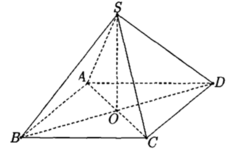
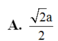
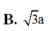
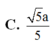
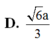
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O cạnh 2a. Thể tích khối chóp S.ABCD bằng 4 a 3 . Tính khoảng cách từ điểm O tới mặt bên của hình chóp.
A. a 2 2
B. 3 a 4
C. 3 a 10 10
D. a 10 10
Chọn C.
Phương pháp
Sử dụng quan hệ vuông góc giữa đường thẳng và mặt phẳng để xác định khoảng cách
Ta tính SO dựa vào công thức thể tích hình chóp, tính OH dựa vào hệ thức lượng trong tam giác vuông.
Cách giải:
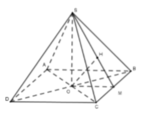
Xét tam giác SOM vuông tại M có OH là đường cao nên theo hệ thức lượng trong tam giác vuông ta có
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O cạnh 2a. Thể tích khối chóp S.ABCD bằng
4
a
3
. Tính khoảng cách từ điểm O tới mặt bên của hình chóp.
Đọc tiếp
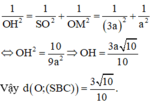
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O cạnh 2a. Thể tích khối chóp S.ABCD bằng 4 a 3 . Tính khoảng cách từ điểm O tới mặt bên của hình chóp.
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng
3
6
, chiều cao bằng
3
3
. Khoảng cách từ đỉnh C đến mặt phẳng (SAB) bằng A. 6 B.
3
2
C. 3 D.
2
3
Đọc tiếp
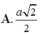
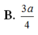
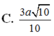
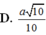
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 3 6 , chiều cao bằng 3 3 . Khoảng cách từ đỉnh C đến mặt phẳng (SAB) bằng
A. 6
B. 3 2
C. 3
D. 2 3
Gọi O là giao điểm của AC và BD. Có
Ta có OA, OB, OS đôi một vuông góc nên với ta có
Chọn đáp án A.
Đúng 0
Bình luận (0)