Trong không gian Oxyz, cho ba điểm không thẳng hàng: A(1; 2; 3), B(−1; 3; 4), C(2; −1; 2).
a) Hãy chỉ ra một cặp vectơ chỉ phương của mặt phẳng (ABC).
b) Viết phương trình mặt phẳng (ABC).
Những câu hỏi liên quan
Trong không gian Oxyz cho ba điểm A(-1;1;2), B(0;1;-1), C(x+2;y;-2) thẳng hàng. Tổng x+y bằng
Trong không gian Oxyz, cho bốn điểm A(-1;2;0), B(3;1;0), C(0;2;1), D(1;2;2). Trong đó có ba điểm thẳng hàng là
A. A, C, D
B. A, B, D
C. B, C, D
D. A, B, C
Trong không gian Oxyz, cho ba điểm không thẳng hàng A(0;1;1), B(-1;0;2), C(-1;1;0). Bán kính đường tròn nội tiếp tam giác ABC bằng A.
6
5
+
3
+
2
.
B.
6
2...
Đọc tiếp
Trong không gian Oxyz, cho ba điểm không thẳng hàng A(0;1;1), B(-1;0;2), C(-1;1;0). Bán kính đường tròn nội tiếp tam giác ABC bằng
A. 6 5 + 3 + 2 .
B. 6 2 5 + 3 + 2 .
C. 2 6 5 + 3 + 2 .
D. 6 . 5 + 3 + 2 .
Đáp án A
Gọi r là bán kính đường tròn nội tiếp tam giác ABC, 2p là chu vi của tam giác đó thì
Đúng 0
Bình luận (0)
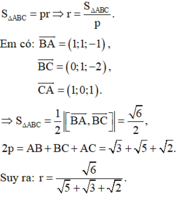
Trong không gian Oxyz, cho ba điểm A(3;5;-1), B(7;x;1), C(9;2;y). Để A, B, C thẳng hàng thì giá trị x+y bằng
A. 5
B. 6
C. 4
D. 7
Trong không gian Oxyz, cho ba điểm
A
(
2
;
5
;
3
)
,
B
(
3
;
7
;
4
)
,
C
(
x
;
y
;
6
)
.
Giá trị của x, y để ba điểm A, B, C thẳng hàng là A. x 5; y 11. B. x -5; y 11. C. x -11; y -5. D. x 11; y 5
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A ( 2 ; 5 ; 3 ) , B ( 3 ; 7 ; 4 ) , C ( x ; y ; 6 ) . Giá trị của x, y để ba điểm A, B, C thẳng hàng là
A. x = 5; y = 11.
B. x = -5; y = 11.
C. x = -11; y = -5.
D. x = 11; y = 5
Trong không gian Oxyz, cho ba điểm
A
(
2
;
5
;
3
)
;
B
(
3
;
7
;
4
)
;
C
(
x
,
y
,
6
)
.
Giá trị của x, y để ba điểm A; B; C thẳng hàng là A. x 5;y 11. B. x -5;y 11. C. x -11;y -5. D. x 11;y 5
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A ( 2 ; 5 ; 3 ) ; B ( 3 ; 7 ; 4 ) ; C ( x , y , 6 ) . Giá trị của x, y để ba điểm A; B; C thẳng hàng là
A. x = 5;y = 11.
B. x = -5;y = 11.
C. x = -11;y = -5.
D. x = 11;y = 5
Chọn A.
Để 3 điểm A, B, C thẳng hàng khi và chi khi A B → , A C → cùng phương
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho ba điểm
A
(
2
;
5
;
3
)
,
B
(
3
;
7
;
4
)
,
C
(
x
;
y
;
6
)
.
Giá trị của x, y để ba điểm A, B, C thẳng hàng là A. x 5; y 11. B. x -5; y 11. C. x -11; y -5. D. x 11; y 5
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A ( 2 ; 5 ; 3 ) , B ( 3 ; 7 ; 4 ) , C ( x ; y ; 6 ) . Giá trị của x, y để ba điểm A, B, C thẳng hàng là
A. x = 5; y = 11.
B. x = -5; y = 11.
C. x = -11; y = -5.
D. x = 11; y = 5
Trong không gian Oxyz, cho ba điểm A(-6;0;0), B(0;-4;0), C(0;0;6). Tập hợp tất cả các điểm M trong không gian cách đều ba điểm A, B, C là một đường thẳng có phương trình là
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(-6;0;0), B(0;-4;0), C(0;0;6). Tập hợp tất cả các điểm M trong không gian cách đều ba điểm A, B, C là một đường thẳng có phương trình là
Chọn đáp án C.
Gọi M(x;y;z) ta có
hệ điều kiện
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(2;-1;3), B(-10;5;3) và M(2m-1;2;n+2). Để A, B, M thẳng hàng thì giá trị của m, n là A.
m
1
,
n
3
2
B.
m
-
3
2
,
n
1
C.
m
...
Đọc tiếp
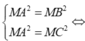
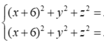
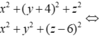
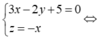
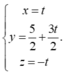
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(2;-1;3), B(-10;5;3) và M(2m-1;2;n+2). Để A, B, M thẳng hàng thì giá trị của m, n là
A. m = 1 , n = 3 2
B. m = - 3 2 , n = 1
C. m = - 1 , n = - 3 2
D. m = 2 3 , n = 3 2
Trong không gian Oxyz cho điểm
M
o
(1; 2; 3) và hai điểm
M
1
(1 + t; 2 + t; 3 + t),
M
2
(1 + 2t; 2 + 2t; 3 + 2t) di động với tham số t. Hãy chứng tỏ ba điểm
M
o
,
M
1
,
M
2
luôn thẳng hàng.
Đọc tiếp
Trong không gian Oxyz cho điểm M o (1; 2; 3) và hai điểm M 1 (1 + t; 2 + t; 3 + t), M 2 (1 + 2t; 2 + 2t; 3 + 2t) di động với tham số t. Hãy chứng tỏ ba điểm M o , M 1 , M 2 luôn thẳng hàng.
