Chọn A.
![]()
Để 3 điểm A, B, C thẳng hàng khi và chi khi A B → , A C → cùng phương
![]()
Chọn A.
![]()
Để 3 điểm A, B, C thẳng hàng khi và chi khi A B → , A C → cùng phương
![]()
Trong không gian Oxyz, cho ba điểm A ( 2 ; 5 ; 3 ) , B ( 3 ; 7 ; 4 ) , C ( x ; y ; 6 ) . Giá trị của x, y để ba điểm A, B, C thẳng hàng là
A. x = 5; y = 11.
B. x = -5; y = 11.
C. x = -11; y = -5.
D. x = 11; y = 5
Trong không gian Oxyz, cho ba điểm A ( 2 ; 5 ; 3 ) , B ( 3 ; 7 ; 4 ) , C ( x ; y ; 6 ) . Giá trị của x, y để ba điểm A, B, C thẳng hàng là
A. x = 5; y = 11.
B. x = -5; y = 11.
C. x = -11; y = -5.
D. x = 11; y = 5
Trong không gian với hệ tọa độ Oxyz cho A ( x ; y ; - 3 ) , B ( 6 ; - 2 ; 4 ) , C ( - 3 ; 7 ; - 5 ) . Giá trị x, y để A, B, C thẳng hàng là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho ba điểm A(3;5;-1), B(7;x;1), C(9;2;y). Để A, B, C thẳng hàng thì giá trị x+y bằng
A. 5
B. 6
C. 4
D. 7
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(8;5;-11), B(5;3;-4), C(1;2;-6) và mặt ( S ) : ( x - 2 ) 2 + ( y - 4 ) 2 + ( z - 1 ) 2 = 9 . Gọi điểm M(a;b;c) là điểm trên (S) sao cho M A → - M B → - M C → đạt giá trị nhỏ nhất. Hãy tìm a+b
A. 6
B. 2
C. 4
D. 9
Trong không gian với hệ tọa độ Oxyz, cho điểm A(-4;1;3) và đường thẳng d : x + 1 - 2 = y - 1 1 = z + 3 3 . B là điểm có tọa độ nguyên trên d sao cho A B = 5 . Tìm tọa độ điểm B.
![]()
![]()

![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;1) và hai đường thẳng d 1 : x - 1 1 = y + 1 1 = z - 3 - 1 ; d 2 : x - 1 1 = y + 2 1 = z - 2 1 . Viết phương trình đường thẳng d song song với mặt phẳng (P):2x+3y+4z-6=0, cắt đường thẳng d1, d2 lần lượt tại M và N sao cho A M ⇀ . A N ⇀ = 5 và điểm N có hoành độ nguyên.
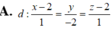
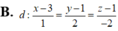
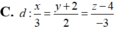
![]()
Trong không gian Oxyz cho ba điểm A(-1;1;2), B(0;1;-1), C(x+2;y;-2) thẳng hàng. Tổng x+y bằng
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(3;-2;3), B(1;0;5) và đường thẳng d : x - 1 1 = y - 2 - 2 = z - 3 2 . Tìm tọa độ điểm M trên đường thẳng (d) để M A 2 + M B 2 đạt giá trị nhỏ nhất.
A. M(2;0;5)
B. M(1;2;3)
C. M(3;-2;7)
D. M(3;0;4)