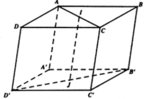
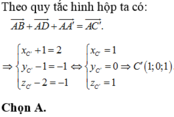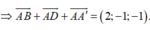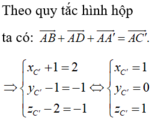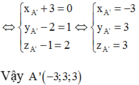Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ và các điểm A(2; 3; 1), C(−1; 2; 3) và O′(1; −2; 2). Tìm tọa độ các đỉnh còn lại của hình hộp.

Những câu hỏi liên quan
Trong Oxyz cho A(0; 2; 0); C(2; 0; 0); O’(0; 0; 3). Khi đó hình hộp OABC.O’A’B’C’ có bao nhiêu mặt phẳng đối xứng?
Đọc tiếp
Trong Oxyz cho A(0; 2; 0); C(2; 0; 0); O’(0; 0; 3). Khi đó hình hộp OABC.O’A’B’C’ có bao nhiêu mặt phẳng đối xứng?
![]()
![]()
![]()
![]()
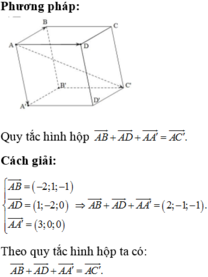
Trong không gian tọa độ Oxyz cho hình hộp ABCD.A’B’C’D’ với các điểm A(-1;1;2), B(-3;2;1), D(0;-1;2) và A(2;1;2). Tìm tọa độ đỉnh C’
Đọc tiếp
Trong không gian tọa độ Oxyz cho hình hộp ABCD.A’B’C’D’ với các điểm A(-1;1;2), B(-3;2;1), D(0;-1;2) và A(2;1;2). Tìm tọa độ đỉnh C’
![]()
![]()
![]()
![]()
Trong không gian tọa độ Oxyz cho hình hộp ABCD.ABCD với các điểm A(-1;1;2), B(-3;2;1), D(0;-1;2) và A(2;1;2) Tìm tọa độ đỉnh C
Đọc tiếp
Trong không gian tọa độ Oxyz cho hình hộp ABCD.A'B'C'D với các điểm A(-1;1;2), B(-3;2;1), D(0;-1;2) và A'(2;1;2) Tìm tọa độ đỉnh C'
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết tọa độ các đỉnh A(-3;2;1), C(4;2;0), B’(-2;1;1), D’(3;5;4). Tìm tọa độ điểm A’ của hình hộp. A. A’(-3;2;1) B. A’(-3;-3;3) C. A’(-3;-3;-3) D. A’(-3;3;3)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết tọa độ các đỉnh A(-3;2;1), C(4;2;0), B’(-2;1;1), D’(3;5;4). Tìm tọa độ điểm A’ của hình hộp.
A. A’(-3;2;1)
B. A’(-3;-3;3)
C. A’(-3;-3;-3)
D. A’(-3;3;3)
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết tọa độ các đỉnh A(-3;2;1), C(4;2;0), B'(-2;1;1), D'(3;5;4). Tìm tọa độ điểm A’ của hình hộp
A. A'(-3;3;1)
B. A'(-3;-3;3)
C. A'(-3;-3;-3)
D. A'(-3;3;3)
Trong không gian Oxyz, cho hình hộp ABCD.ABCD có A(1;0;0), B(1;2;0), D(2;-1;0), A’(5;2;2). Tọa độ điểm C’ là: A. (3;1;0) B. (8;3;2) C. (2;1;0) D. (6;3;2)
Đọc tiếp
Trong không gian Oxyz, cho hình hộp ABCD.A'B'C'D' có A(1;0;0), B(1;2;0), D(2;-1;0), A’(5;2;2). Tọa độ điểm C’ là:
A. (3;1;0)
B. (8;3;2)
C. (2;1;0)
D. (6;3;2)
Đáp án D
Vì ACC’A’, ABCD là những hình bình hành nên áp dụng quy tắc hình bình hành ta có:
![]()
Từ đó suy ra:
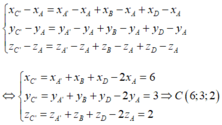
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hình hộp ABCD.ABCD có A(0;0;0), B(1;2;0), D(2;-1;0), A’(5;2;3). Tọa độ của điểm C’ là: A. (3;1;0) B. (8;3;3) C. (-8;-3;-3) D. (-2;-1;-3)
Đọc tiếp
Trong không gian Oxyz, cho hình hộp ABCD.A'B'C'D' có A(0;0;0), B(1;2;0), D(2;-1;0), A’(5;2;3). Tọa độ của điểm C’ là:
A. (3;1;0)
B. (8;3;3)
C. (-8;-3;-3)
D. (-2;-1;-3)
Trong không gian với hệ tọa độ Oxyz cho hình hộp ABCD.ABCD. Biết A(2;4;0), B(4;0;0), C(-1;4;-7) và D(6;8;10). Tọa độ điểm B là A. B(8;4;10) B. B(6;12;0) C. B(10;8;6) D. B(13;0;17)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hình hộp ABCD.A'B'C'D'. Biết A(2;4;0), B(4;0;0), C(-1;4;-7) và D(6;8;10). Tọa độ điểm B' là
A. B'(8;4;10)
B. B'(6;12;0)
C. B'(10;8;6)
D. B'(13;0;17)
Trong không gian Oxyz cho hình hộp chữ nhật OABC.ÈGH có các cạnh OA5, OC8, OE7 (xem hình vẽ). Hãy tìm tọa độ điểm H. A. H (0;7;8) B. H( 7;8;0) C. H (8;7;0) D. (0;8;7)
Đọc tiếp
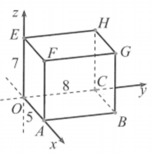
Trong không gian Oxyz cho hình hộp chữ nhật OABC.ÈGH có các cạnh OA=5, OC=8, OE=7 (xem hình vẽ). Hãy tìm tọa độ điểm H.
A. H (0;7;8)
B. H( 7;8;0)
C. H (8;7;0)
D. (0;8;7)
Trong không gian Oxyz cho hình hộp chữ nhật OABC.EFGH có các cạnh OA5, OB8, OE7 (xem hình vẽ). Hãy tìm tọa độ điểm H. A. H(0;7;8) B. H(7;8;0) C. H(8;7;0) D. H(0;8;7)
Đọc tiếp
Trong không gian Oxyz cho hình hộp chữ nhật OABC.EFGH có các cạnh OA=5, OB=8, OE=7 (xem hình vẽ). Hãy tìm tọa độ điểm H.
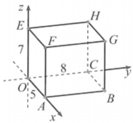
A. H(0;7;8)
B. H(7;8;0)
C. H(8;7;0)
D. H(0;8;7)
Ta có H ∈ ( y O z ) là hình chiếu của H lên Oy trùng với C nên H(0;8;7).
Chọn D
Đúng 0
Bình luận (0)